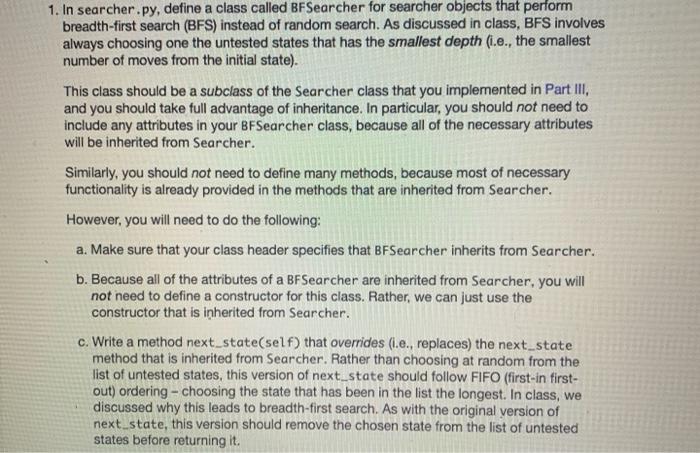
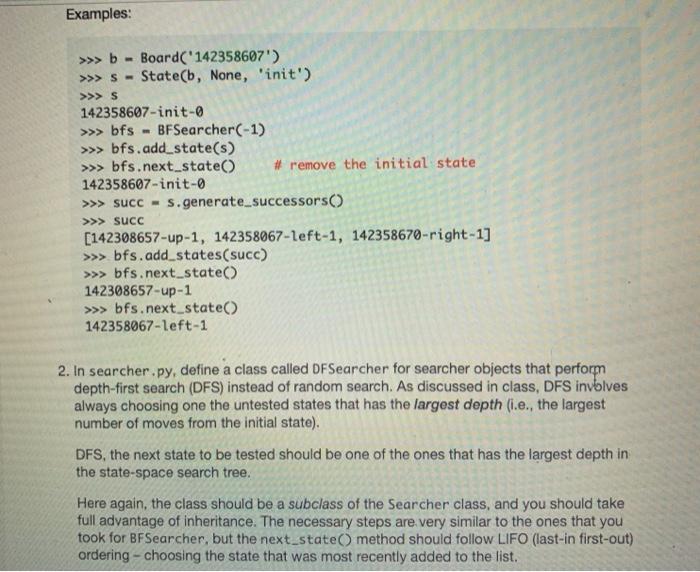
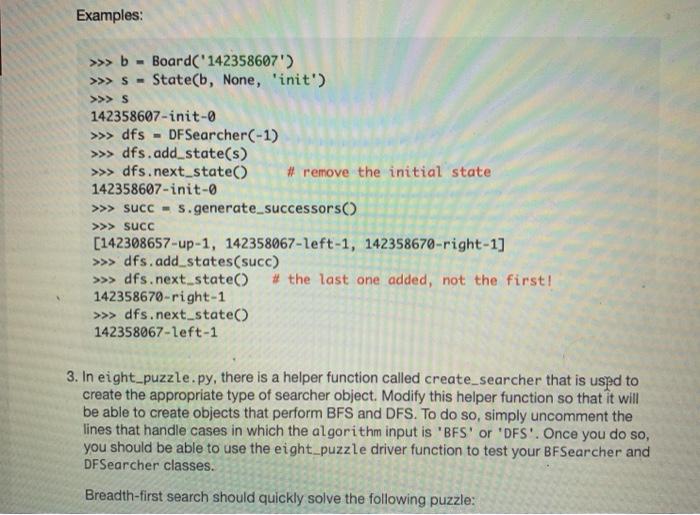
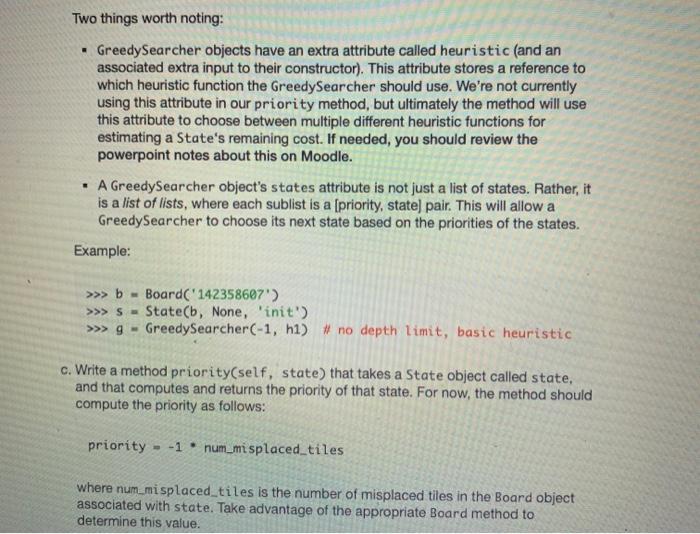
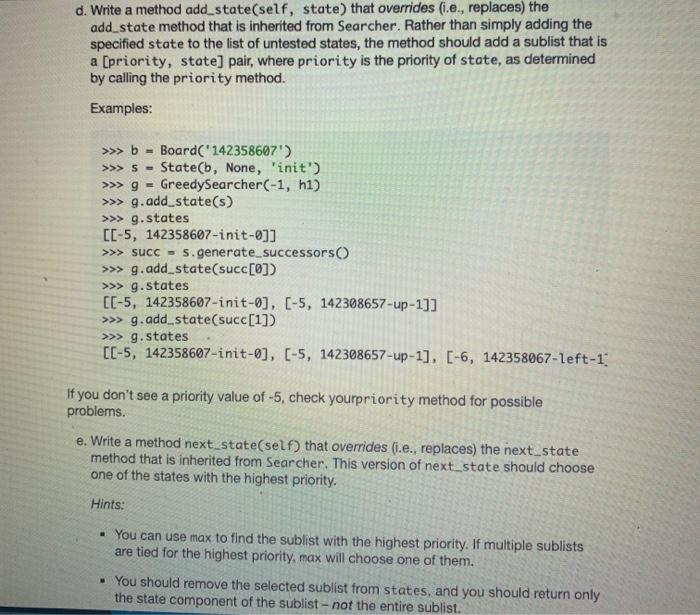
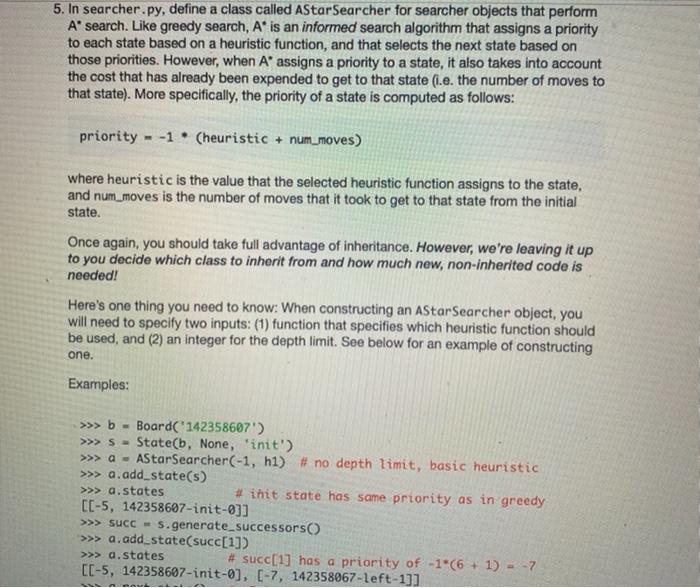
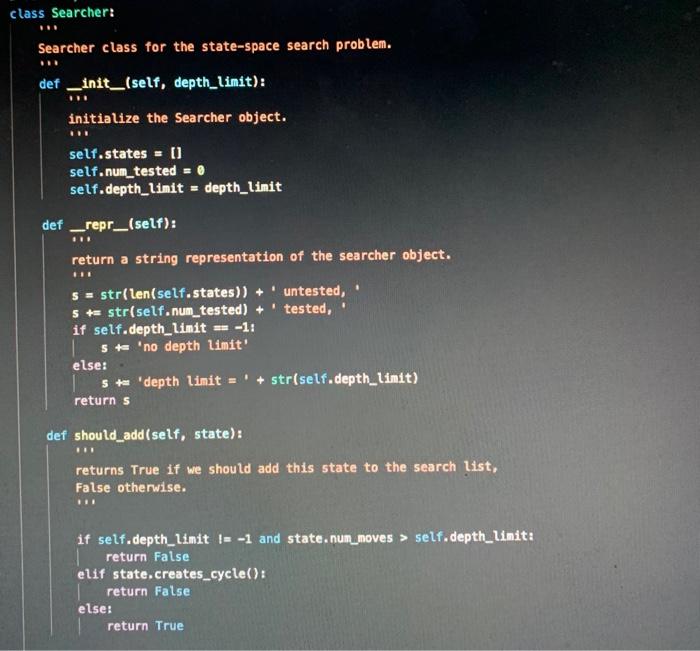
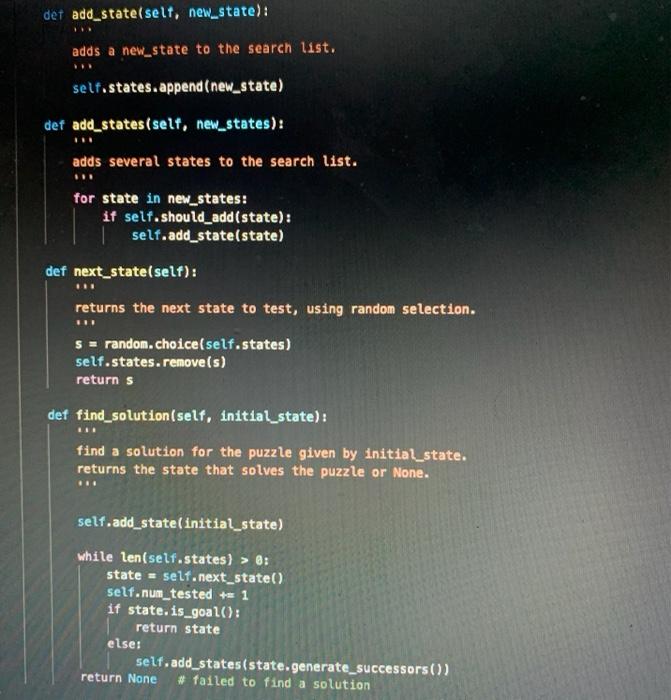
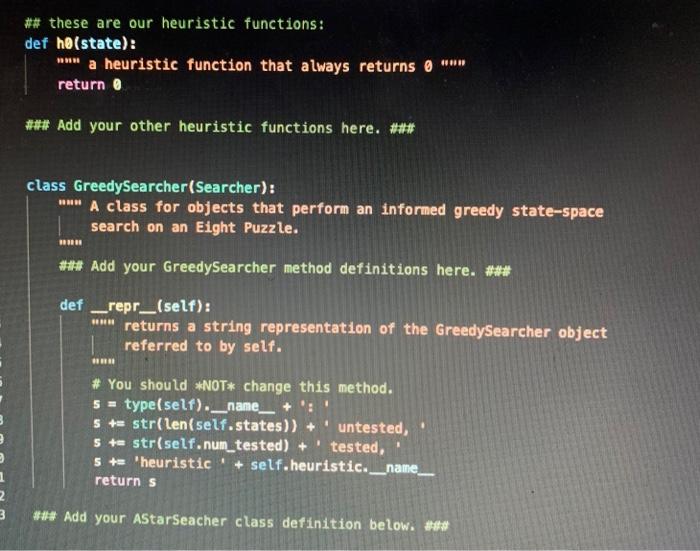
1. In searcher.py, define a class called BFSearcher for searcher objects that perform breadth-first search (BFS) instead of random search. As discussed in class, BFS involves always choosing one the untested states that has the smallest depth (i.e., the smallest number of moves from the initial state). This class should be a subclass of the Searcher class that you implemented in Part III, and you should take full advantage of inheritance. In particular, you should not need to include any attributes in your BFSearcher class, because all of the necessary attributes will be inherited from Searcher. Similarly, you should not need to define many methods, because most of necessary functionality is already provided in the methods that are inherited from Searcher. However, you will need to do the following: a. Make sure that your class header specifies that BFSearcher inherits from Searcher. b. Because all of the attributes of a BFSearcher are inherited from Searcher, you will not need to define a constructor for this class. Rather, we can just use the constructor that is inherited from Searcher. c. Write a method next_state(self) that overrides (i.e., replaces) the next_state method that is inherited from Searcher. Rather than choosing at random from the list of untested states, this version of next state should follow FIFO (first-in first- out) ordering - choosing the state that has been in the list the longest. In class, we discussed why this leads to breadth-first search. As with the original version of next state, this version should remove the chosen state from the list of untested states before returning it. Examples: >>> b Board('142358607') - >>>5- State(b, None, 'init') >>> S 142358607-init-0 >>> bfs BFSearcher(-1) >>> bfs.add_state(s) >>> bfs.next_state() 142358607-init-0 - #remove the initial state >>> succ=s.generate_successors() >>> SUCC [142308657-up-1, 142358067-left-1, 142358670-right-1] >>> bfs.add_states (succ) >>> bfs.next_state() >>> bfs.next_state() 142358067-left-1 142308657-up-1 2. In searcher.py, define a class called DFSearcher for searcher objects that perform depth-first search (DFS) instead of random search. As discussed in class, DFS involves always choosing one the untested states that has the largest depth (i.e., the largest number of moves from the initial state). DFS, the next state to be tested should be one of the ones that has the largest depth in the state-space search tree. Here again, the class should be a subclass of the Searcher class, and you should take full advantage of inheritance. The necessary steps are very similar to the ones that you took for BFSearcher, but the next_state() method should follow LIFO (last-in first-out) ordering - choosing the state that was most recently added to the list. Examples: >>> b Board('142358607') >>> S- State(b, None, 'init') >>> S - 142358607-init-0 >>> dfs - DFSearcher(-1) >>> dfs.add_state(s) >>> dfs.next_state() # remove the initial state 142358607-init-0 >>> succ=s.generate_successors() >>> succ [142308657-up-1, 142358067-left-1, 142358670-right-1] >>> dfs.add_states (succ) >>> dfs.next_state() #the last one added, not the first! 142358670-right-1 >>> dfs.next_state() 142358067-left-1 3. In eight_puzzle.py, there is a helper function called create_searcher that is used to create the appropriate type of searcher object. Modify this helper function so that it will be able to create objects that perform BFS and DFS. To do so, simply uncomment the lines that handle cases in which the algorithm input is 'BFS' or 'DFS'. Once you do so, you should be able to use the eight_puzzle driver function to test your BFSearcher and DFSearcher classes. Breadth-first search should quickly solve the following puzzle: >>> eight_puzzle('142358607', 'BFS', -1) BFS: 0.006 seconds, 56 states Found a solution requiring 5 moves. Show the moves (y/n)? You may get a different time than we did, but the rest of the results should be the same. As discussed in class, BFS finds an optimal solution for eight-puzzle problems, so 5 moves is the fewest possible moves for this particular initial state. Depth-first search, on the other hand, ends up going deep in the search tree before it finds a goal state: >>> eight puzzle('142358607', 'DFS', -1) DFS: 10.85 seconds, 3100 states. Found a solution requiring 3033 moves. Show the moves (y/n)? Important: In cases like this one in which the solution has an extremely large number of moves, trying to show the moves is likely to cause an error. That's because our print_moves_to method uses recursion, and the number of recursive calls is equal to the number of moves in the solution. Each recursive call adds a new stack frame to the top of the memory stack, and we can end up overflowing the stack when we make that many recursive calls. To get a solution from DFS with fewer moves, we can impose a depth limit by passing it in as the third argument to the eight_puzzle function. For example: >>> eight puzzle('142358607', 'DFS, 25) DFS: 6.945 seconds, 52806 states Found a solution requiring 23 moves. Show the moves (y/n)? 4. In searcher.py, define a class called GreedySearcher for searcher objects that perform greedy search. As discussed in class, greedy search is an informed search algorithms that uses a heuristic function to estimate the remaining cost needed to get from a given state to the goal state (for the Eight Puzzle, this is just an estimate of how many additional moves are needed). Greedy Search uses this heuristic function to assign a priority to each state, and it selects the next state based on those priorities. Once again, this class should be a subclass of the Searcher class that you implemented in Part III, and you should take full advantage of inheritance. However, the changes required in this class will be more substantial that the ones in BFSearcher and DFSearcher. Among other things, GreedySearcher objects will have a new attribute called heuristic that will allow you to choose among different heuristic functions, and they will also have a new method for computing the priority of a state. Here are the necessary steps: a. Make sure that your class header specifies that GreedySearcher inherits from Searcher. b. Define the constructor for the Greedy Searcher class. Copy the following code into the GreedySearcher class: def _init__(self, depth_limit, heuristic): constructor for a GreedySearcher object inputs: depth limit the depth limit of the searcher * heuristic a reference to the function that should be when computing the priority of a state www www. - # add code that calls the superclass constructor. self.heuristic A heuristic Two things worth noting: GreedySearcher objects have an extra attribute called heuristic (and an associated extra input to their constructor). This attribute stores a reference to which heuristic function the GreedySearcher should use. We're not currently using this attribute in our priority method, but ultimately the method will use this attribute to choose between multiple different heuristic functions for estimating a State's remaining cost. If needed, you should review the powerpoint notes about this on Moodle. A GreedySearcher object's states attribute is not just a list of states. Rather, it is a list of lists, where each sublist is a [priority, state] pair. This will allow a GreedySearcher to choose its next state based on the priorities of the states. Example: >>> b= Board('142358607') >>> S >>> g- State (b, None, 'init') GreedySearcher(-1, h1) # no depth limit, basic heuristic c. Write a method priority(self, state) that takes a State object called state, and that computes and returns the priority of that state. For now, the method should compute the priority as follows: priority -1 num_misplaced_tiles where num_misplaced_tiles is the number of misplaced tiles in the Board object associated with state. Take advantage of the appropriate Board method to determine this value. d. Write a method add_state(self, state) that overrides (i.e., replaces) the add state method that is inherited from Searcher. Rather than simply adding the specified state to the list of untested states, the method should add a sublist that is a [priority, state] pair, where priority is the priority of state, as determined by calling the priority method. Examples: >>> b= Board('142358607') >>>5- State(b, None, 'init') >>> g = GreedySearcher(-1, h1) >>> g.add_state(s) >>> g.states [[-5, 142358607-init-0]] >>> succ=s.generate successors() >>> g.add_state(succ[0]) >>> g.states [[-5, 142358607-init-0], [-5, 142308657-up-1]] >>> g.add_state(succ[1]) >>> g.states [[-5, 142358607-init-0], [-5, 142308657-up-1], [-6, 142358067-left-1 If you don't see a priority value of -5, check yourpriority method for possible problems. e. Write a method next_state(self) that overrides (i.e., replaces) the next state method that is inherited from Searcher. This version of next state should choose one of the states with the highest priority. Hints: . You can use max to find the sublist with the highest priority. If multiple sublists are tied for the highest priority, max will choose one of them. . You should remove the selected sublist from states, and you should return only the state component of the sublist-not the entire sublist. 5. In searcher.py, define a class called AStar Searcher for searcher objects that perform A search. Like greedy search, A is an informed search algorithm that assigns a priority to each state based on a heuristic function, and that selects the next state based on those priorities. However, when A assigns a priority to a state, it also takes into account the cost that has already been expended to get to that state (i.e. the number of moves to that state). More specifically, the priority of a state is computed as follows: priority --1 (heuristic + num_moves) where heuristic is the value that the selected heuristic function assigns to the state, and num_moves is the number of moves that it took to get to that state from the initial state. Once again, you should take full advantage of inheritance. However, we're leaving it up to you decide which class to inherit from and how much new, non-inherited code is needed! Here's one thing you need to know: When constructing an AStar Searcher object, you will need to specify two inputs: (1) function that specifies which heuristic function should be used, and (2) an integer for the depth limit. See below for an example of constructing one. Examples: >>> b Board('142358607') >>> S- State(b, None, 'init') >>> a AStar Searcher(-1, h1) # no depth limit, basic heuristic >>> a.add_state(s) >>> a.states #ihit state has same priority as in greedy [[-5, 142358607-init-0]] >>> succ=s.generate_successors() >>> a.add_state(succ[1]) >>> a.states #succ[1] has a priority of -1*(6 + 1) = -7 [[-5, 142358607-init-0], [-7, 142358067-left-1]] 6. Modify the create_searcher helper function in eight_puzzle.py so that it will be able to create GreedySearcher and AStar Searcher objects. To do so, simply uncomment the lines that handle cases in which the algorithm input is 'Greedy' or 'A*'. After you do so, try using the eight_puzzle driver function to see how the informed search algorithms perform on various puzzles. Here are some digit strings for puzzles that you might want to try, along with the number of moves in their optimal solutions: '142358607' - 5 moves '031642785' - 8 moves '341682075' - 10 moves 631074852' - 15 moves '763401852' - 18 moves '145803627 - 20 moves A* should obtain optimal solutions; Greedy Search may or may not. If a given algorithm ends up taking longer than you can afford to wait, you can stop it by using Ctrl-C from the keyboard. class Searcher: *** Searcher class for the state-space search problem. def_init_(self, depth_limit): initialize the Searcher object. self.states = [] self.num_tested = 0 self.depth_limit = depth_limit *** def repr_(self): return a string representation of the searcher object. #HE *** s str(len(self.states))+' untested, s += str(self.num_tested) + ' tested, if self.depth_limit === -1: s'no depth limit' else: s+ 'depth limit=' + str(self.depth_limit) return s def should add(self, state): *** returns True if we should add this state to the search list, False otherwise. *** if self.depth limit != -1 and state.num_moves > self.depth_limit: return false elif state.creates_cycle(): return false else: return True det add_state(self, new_state): adds a new state to the search list. self.states.append(new_state) def add_states (self, new_states): 111 adds several states to the search list. 111 for state in new_states: if self.should add (state): self.add_state(state) def next_state(self): returns the next state to test, using random selection. 111 "H s = random.choice (self.states) self.states.remove(s) return s def find solution (self, initial_state): find a solution for the puzzle given by initial state. returns the state that solves the puzzle or None. *** self.add_state(initial_state) while len(self.states) > 8: state= self.next_state() self.num_tested += 1 if state.is_goal(): return state else: self.add_states (state.generate_successors()) return None # failed to find a solution 2 3 ## these are our heuristic functions: def ho(state): """ a heuristic function that always returns @ "*** return 0 ### Add your other heuristic functions here. ### class GreedySearcher (Searcher): BH www A class for objects that perform an informed greedy state-space search on an Eight Puzzle. ### Add your GreedySearcher method definitions here. ### def repr_(self): returns a string representation of the GreedySearcher object referred to by self. www HO # You should *NOT* change this method. 5 = type(self)._name_+': ' s+ str(len(self.states)) + untested, 5+= str(self.num_tested) + tested, 5+= 'heuristic + self.heuristic._name_ return s ### Add your AStarSeacher class definition below. ###