1) Integrate to compute the total charge, Q, on one of the two patches. You can calculate Q on the other patch, as well, and you should expect to get the same magnitude (within less than 2% difference). Note that the geometry and data provided for this final project involve cylindrical coordinates, so make sure to take that into account when integrating the charge density to get the charge. Also, note that the surface charge density is azimuthally symmetric, and only varies with radius.

2) Apply Coulomb's law to calculate the electric field along a path between the two conducting patches. You are encouraged to choose the easiest path, which corresponds to a segment along the ??-axis between the two patches, i.e., on the segment ?? = 0, and 0 ? ?? ? ??. Note that due to the symmetry of this problem, the only non-zero component of the electric field on this path should be Ez. Don't forget that this electric field includes contributions from all the charges (that is, both the positive charges on the upper patch and the negative charges on the lower patch). To avoid singularities in your integral, we recommend that you limit your calculation of Ez(z) to 9 evenly spaced points between 0

3) Integrate your solution for Ez along the path between the two charged patches, to compute the magnitude of the difference in electrostatic potential (the voltage) between the two conductors: In this instance, you will calculate |?V| from Ez(z) using only the 9 z-values at which you calculated Ez in step 2.

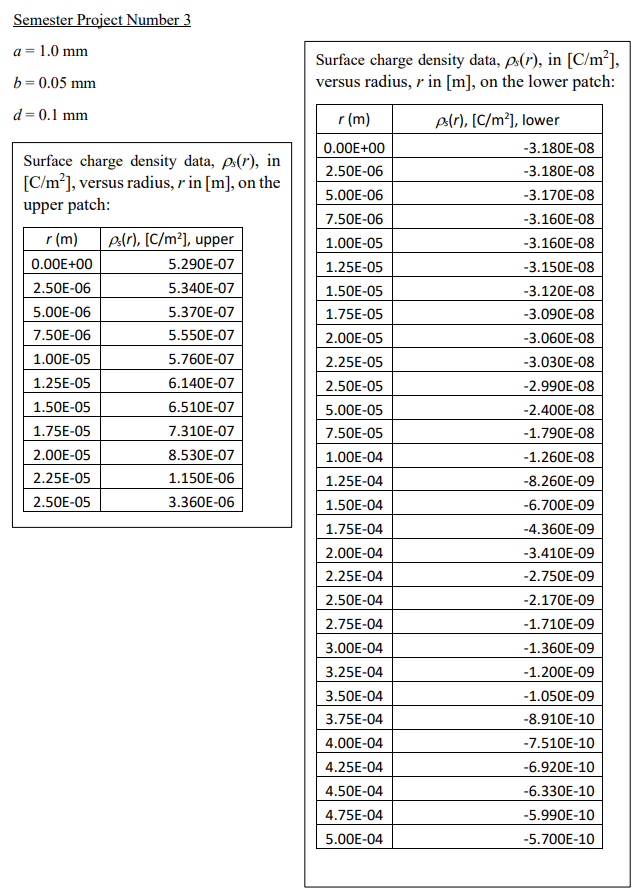
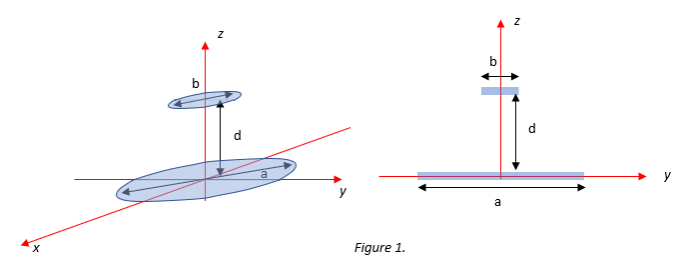
Semester Project Number 3 a = 1.0 mm Surface charge density data, p.(r), in [C/m]], b = 0.05 mm versus radius, / in [m], on the lower patch: d = 0.1 mm r (m) ps(r), [C/m'], lower 0.00E+00 -3.180E-08 Surface charge density data, ps(r), in 2.50E-06 -3.180E-08 [C/m ], versus radius, r in [m], on the 5.00E-06 -3.170E-08 upper patch: 7.50E-06 3.160E-08 r (m) ps(r), [C/m2], upper 1.00E-05 -3.160E-08 0.00E+00 5.290E-07 1.25E-05 -3.150E-08 2.50E-06 5.340E-07 1.50E-05 -3.120E-08 5.00E-06 5.370E-07 1.75E-05 -3.090E-08 7.50E-06 5.550E-07 2.00E-05 -3.060E-08 1.00E-05 5.760E-07 2.25E-05 -3.030E-08 1.25E-05 6.140E-07 2.50E-05 -2.990E-08 1.50E-05 6.510E-07 5.00E-05 -2.400E-08 1.75E-05 7.310E-07 7.50E-05 -1.790E-08 2.00E-05 8.530E-07 1.00E-04 -1.260E-08 2.25E-05 1.150E-06 1.25E-04 -8.260E-09 2.50E-05 3.360E-06 1.50E-04 -6.700E-09 1.75E-04 -4.360E-09 2.00E-04 -3.410E-09 2.25E-04 -2.750E-09 2.50E-04 -2.170E-09 2.75E-04 -1.710E-09 3.00E-04 -1.360E-09 3.25E-04 -1.200E-09 3.50E-04 -1.050E-09 3.75E-04 -8.910E-10 4.00E-04 -7.510E-10 4.25E-04 -6.920E-10 4.50E-04 -6.330E-10 4.75E-04 -5.990E-10 5.00E-04 -5.700E-10\fZ Z b b d d a y e X Figure 1