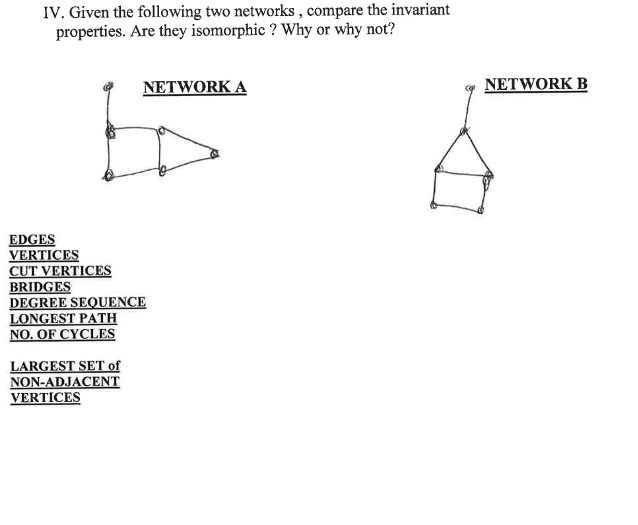
$1.$ IV$.$ Given the followg two networks, compare the invariant

properties. Are they isomorphic? Why or why not?

A$.$ Draw a tree which is both complete bipartite and complete and which has atleast $6$ vertices. If NOT possible say why.

B$.$ Then draw a network which is not a tree but which has $4$ cycles of length $4$ and is bipartite.

C$.$ Then draw a complete bipartite network that is not a tree with degree sequence

$2,2,2,3,3,$

If not possible, indicate so and why.

$2.$ Prove that n is $($a$)($itle o$.)25.-->$ infrit

$3.$ Draw two networks that have $6$ edges, $7$ vertices, are both connected, and have the same degree sequence but which are not isomorphic.

Explain why they are not isomorphic.

$4.$ See photo attached

$5.$ Using the grid below start at the position called $1$ and draw a knight's walk. You are not expected to solve the Knight's Tour. USING this scenario:

$$Always go left before you go right

$$Always go up before you go down

FOR EXAMPLE, if you have four moves... and one is up right and one is up left go up left

If you have two moves left down or right up do the left up