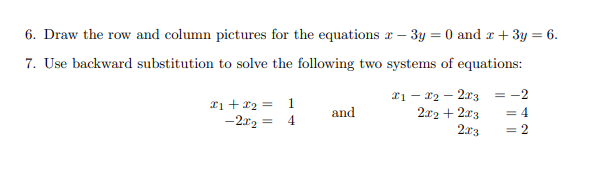
1. Let 1= 2 .0= 1 and w = -2. (a) Check whether u and v are linearly independent or not. (b) What is span of {u, v}? (c) Check whether u and w are linearly independent or not. (d) What is span of {u, w}? (e) What is the span of {u, v, w}? 2. Let (a) Check whether u and v are linearly independent or not. (b) Check whether w is a linear combination of u and v. (c) Check whether a is a linear combination of u and v. (d) Is span of { u, v} = R3? 3. Let u and v be two linearly independent vectors. Let w = u + 2v and x = u - yv. Find y such that w and r are linearly independent. 1. (a) Compute AB. Does BA exist? (b) Compute BC and find B- and C-1. 5. The aim of this exercise is to show that a matrix A times a vector is equivalent to taking a linear combination of the columns of A. Let A = and r = Verify that Ar = $16. Draw the row and column pictures for the equations x - 3y = 0 and + + 3y = 6. 7. Use backward substitution to solve the following two systems of equations: $1 - 12 - 213 = -2 and 2x2 + 213 =4 -212 4 213