Question: 1. Let + and . be the usual binary operations of addition and multiplication on the set Z. And let H = (n' In E

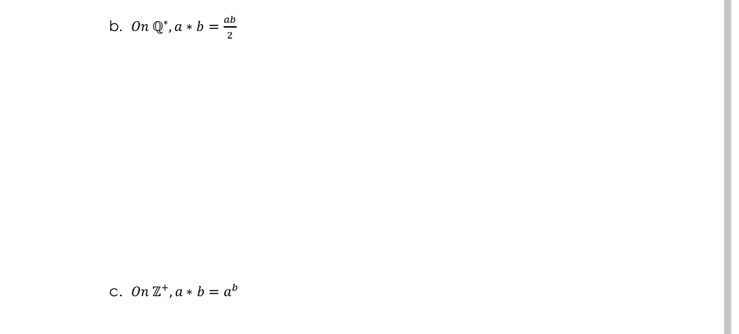
1. Let + and . be the usual binary operations of addition and multiplication on the set Z. And let H = (n' In E Z+), determine whether it is closed under a. Addition b. Multiplication 2. Determine in each case, if the given * is (i) commutative, (ii) associative, and if there is (ii)an identity element e. Now, if e exists, determine the (iv) inverse element. a. On Z, a * b = a + ab\f

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

with detailed solution typewritten 5. Find three relation from {1, 2} to {6, 7} that are NOT functions. 6. 3. Find all relations from {4, 5, 6} to {1, 2}. b. Find all functions from {4, 5, 6} to {1,...

4.1 Questions 10, 17, 21, 22 No plagrism and please write on paper thanks a lot d. Show that Axiom 5 holds by producing a vector -u such that u + (-u) = 0 for u = (u,, uz) e. Find two vector space...

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

I've attached what I have thus far and then the notes that I received back below the questions. I need to prove A1 - A10. Some require specific numeric entries. I attempted this but need to more...

Help me please. In the month of September, all of the walmart grocery stores in Virginia sold 429,382 eggs. In that same month, all of the walmart grocery stores in Texas sold 283,054 eggs. How many...

4. Verify all vector space axioms and determine, if the set of all triples of real numbers (x, y, z) is a vector space under the given operations ( x, y, z) + ( x , y , z ) = (x + x ,yty ,z+z) and...

Yeayyy.com: venturing into mobile app business Gearing up for the future Yeayyy.com was incorporated as a private limited company in February 2010. Its office was located in Bandar Baru Bangi,...

QUESTION 2 (20 marks) What was the business situation of Yeayyy.com by end 2014? Use SWOT-TOWS matrix to support your analysis of the companys situation. Answer ALL FIVE (5) ROWS Zoom Window Macros...

Yeayyy.com: venturing into mobile app business Gearing up for the future Yeayyy.com was incorporated as a private limited company in February 2010. Its office was located in Bandar Baru Bangi,...

7. (Combined loading) The beam shown is loaded in the xy and xz planes. (a) Find the y- and z-components of the reactions at the supports. (b) Plot the shear-force and bending-moment diagrams for the...

2. You have two job offers with the following 6-year compensation terms: the first one offers you $80,000 a year for the next 6 years; the other one offers you a signing bonus of $15,000 plus $50,000...

Investments: Delineating an Efficient Portfolio 1 . Rahul s uncle said he wanted an efficient portfolio with a 1 0 % risk maximum and diversified. How would you define each of those phrases in this...

[The following information applies to the questions displayed below.] As a long-term investment, Painters' Equipment Company purchased 20% of AMC Supplies Inc.'s 550,000 shares for $630,000 at the...