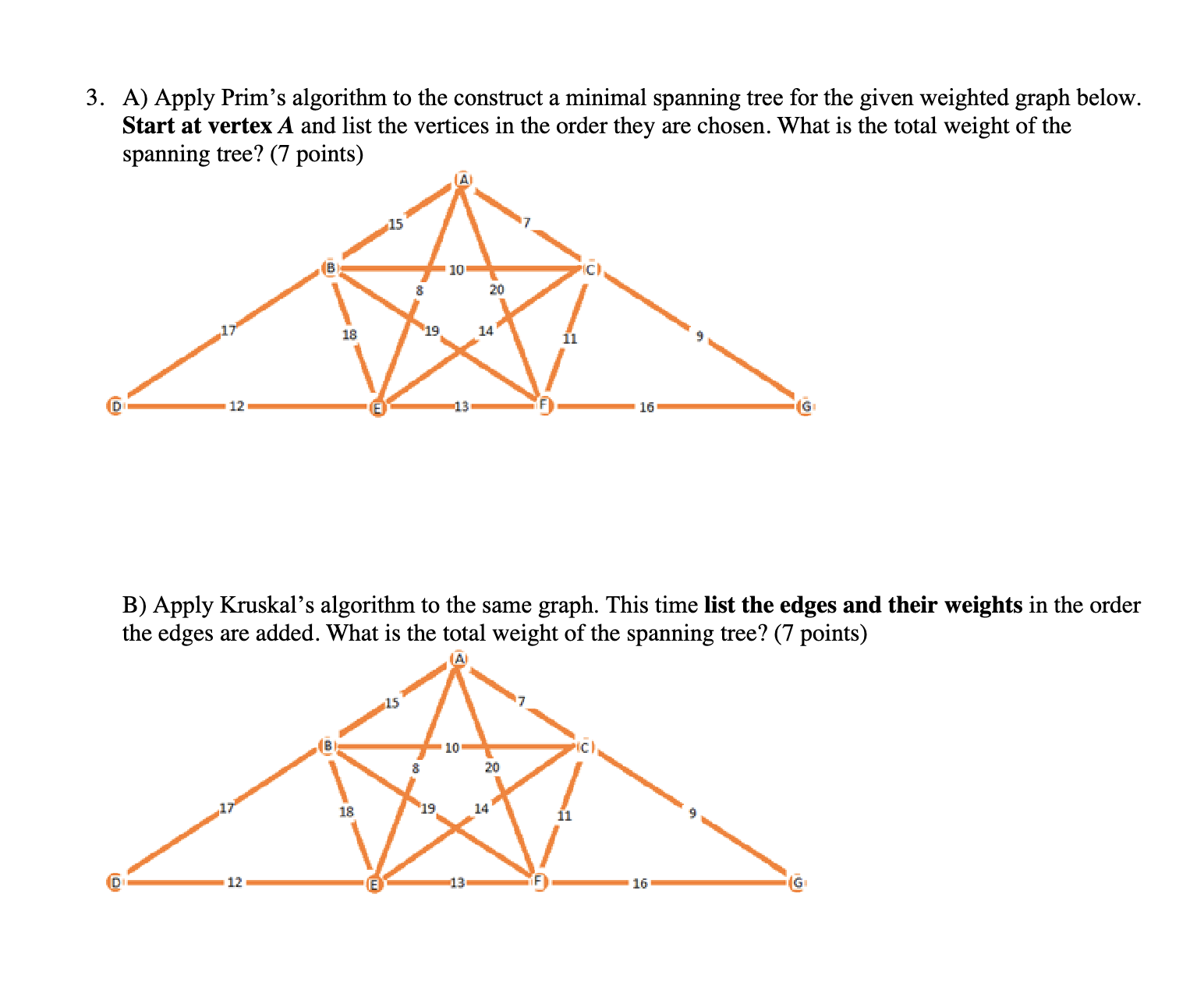
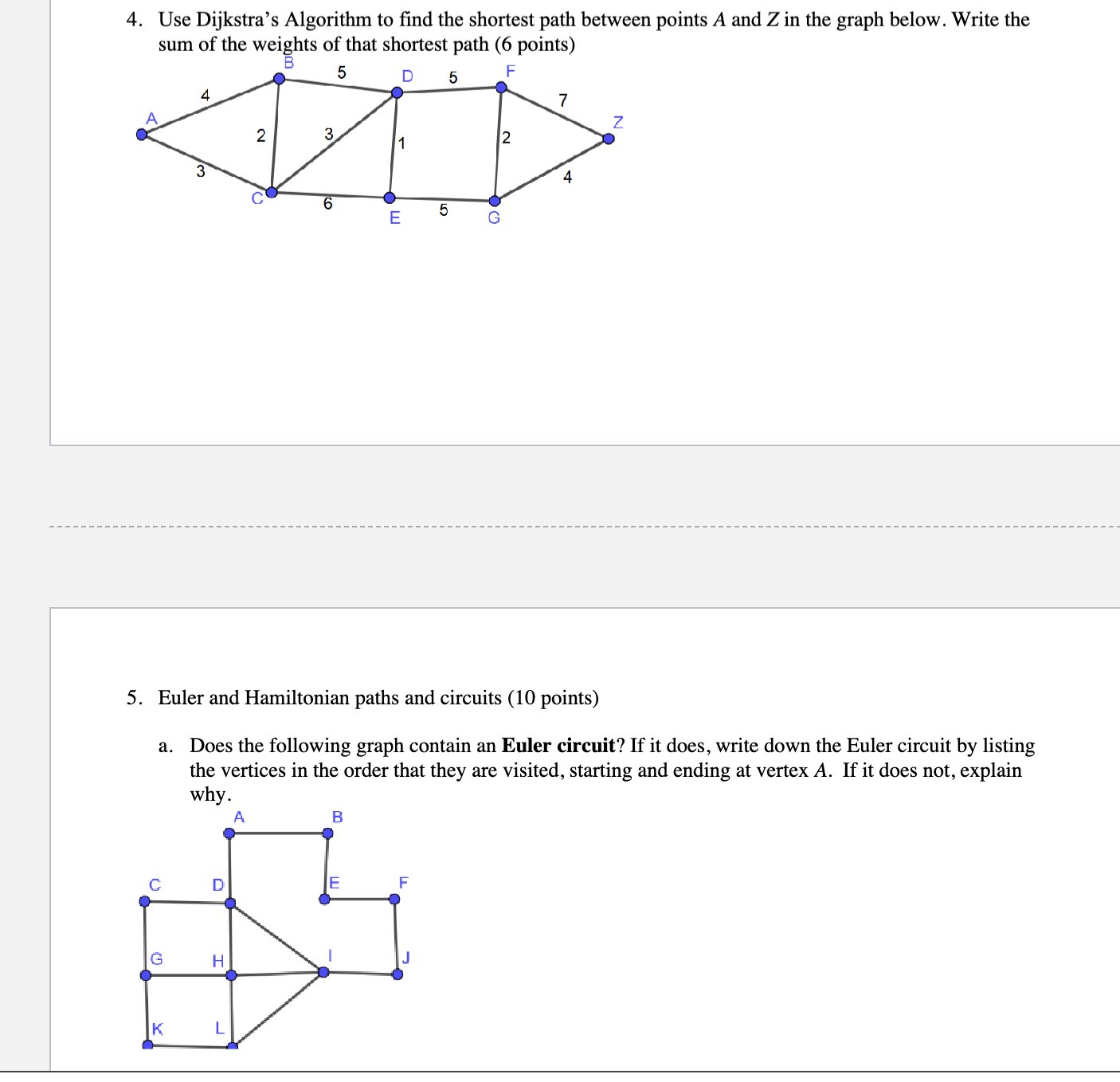
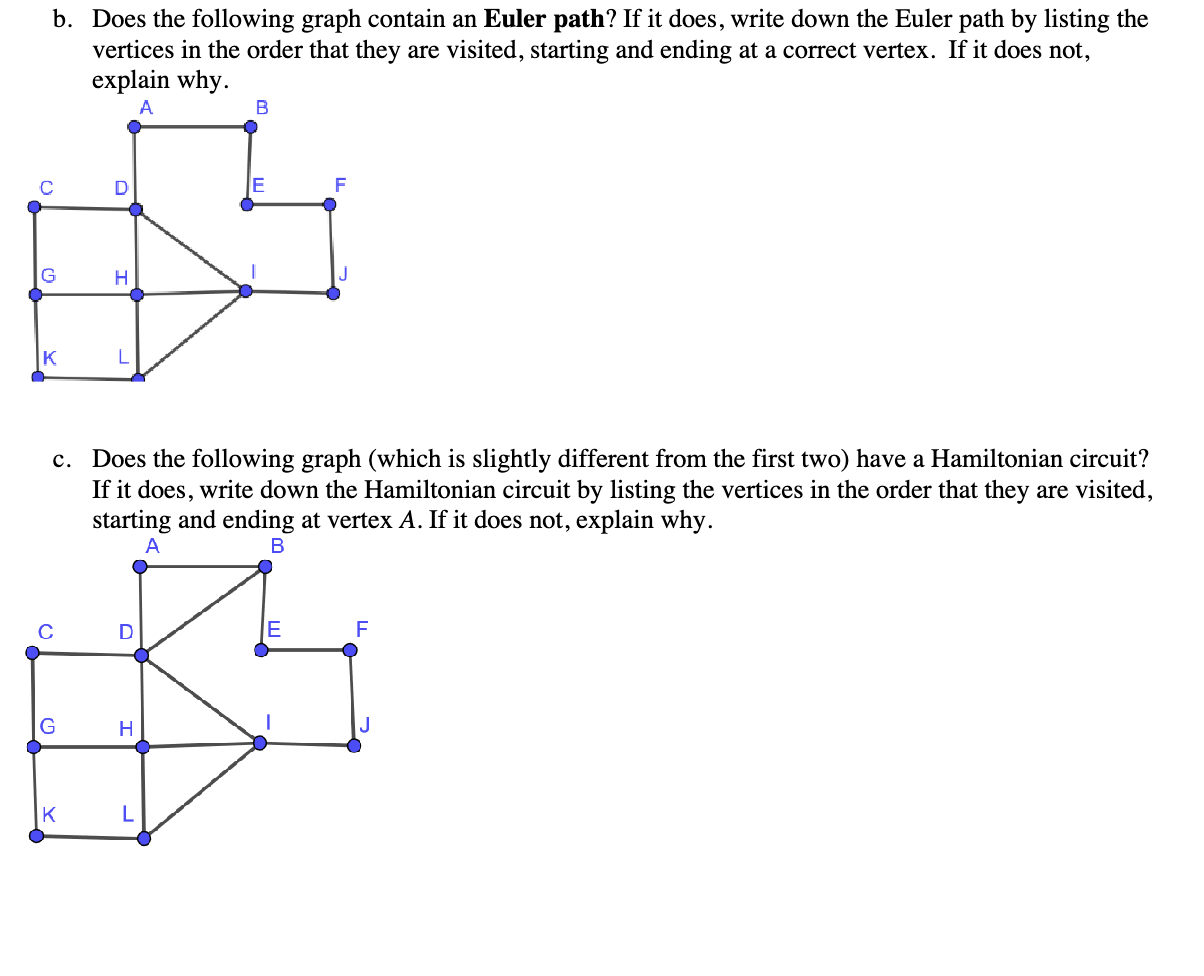
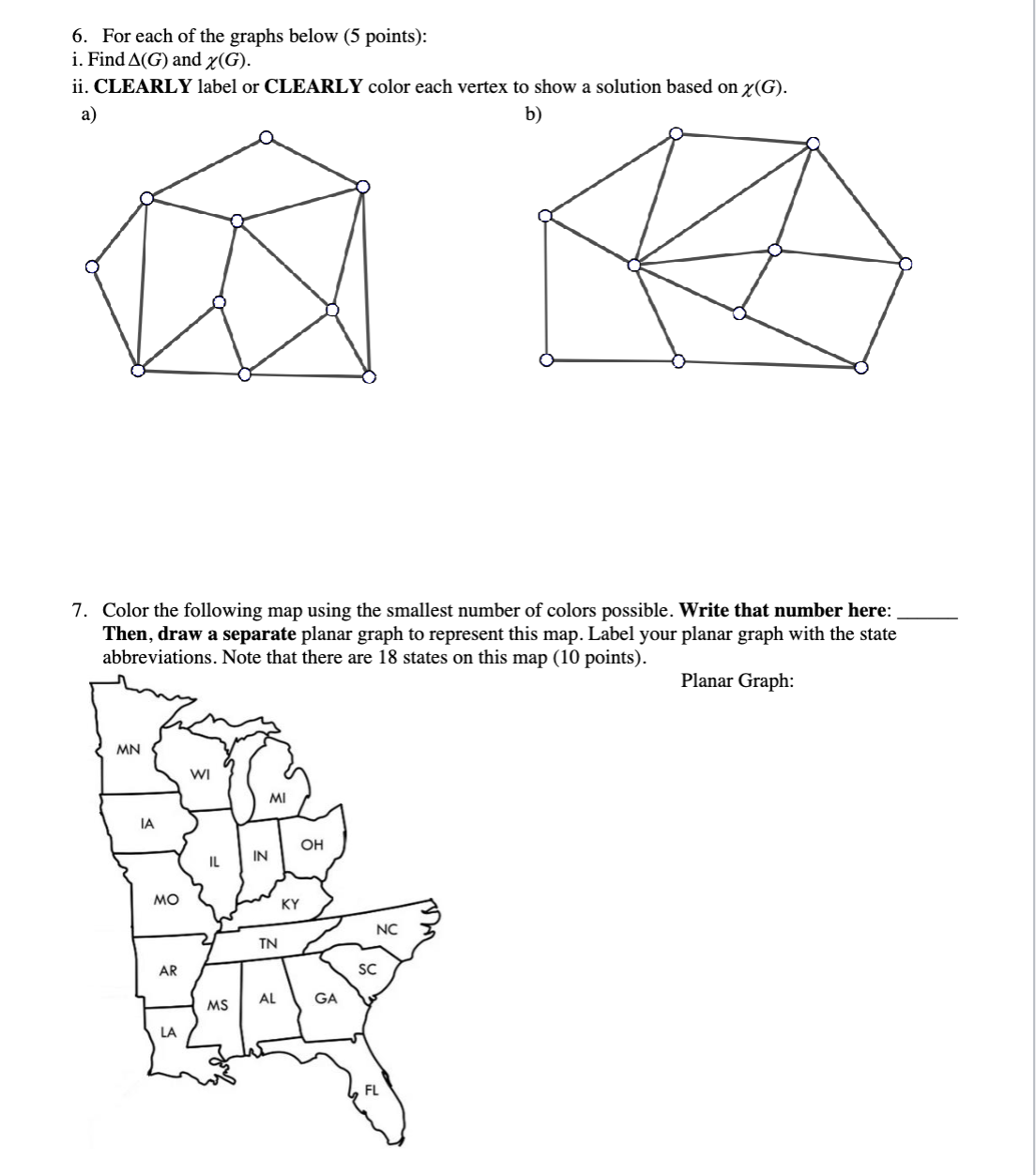
1. Let connected graph G have vertex set V = {A, B, C, D, E} and the edge set as given below. In each situation, draw G with as few crossings as possible. (10 points) a) E1 = {(A, C); (A, D); (B, O); (D, E); (B, D); (B, D); (B, E); (C,E)} b) E2 = {(A, B); (A4, D); (A, C); (A, E); (B, D); (C, E); (D.E); (B,E)} c) for each graph, list three pairs of adjacent vertices (if possible) and three pairs of non-adjacent vertices (if possible). If it is not possible, write \"not possible\". Graph E1: Graph Ex: Three pairs of adjacent vertices are: Three pairs of adjacent vertices are: Three pairs of non-adjacent vertices are: Three pairs of non-adjacent vertices are: 2. Which of the following graphs are bipartite? If they are, write out the two sets A and B that are bipartite. If they are not, explain why. (5 points) a) b) C A B A B e " \\e [ \" . A) Apply Prim's algorithm to the construct a minimal spanning tree for the given weighted graph below. Start at vertex A and list the vertices in the order they are chosen. What is the total weight of the spanning tree? (7 points) B) Apply Kruskal's algorithm to the same graph. This time list the edges and their weights in the order the edges are added. What is the total weight of the spanning tree? (7 points) 4. Use Dijkstra's Algorithm to find the shortest path between points A and Z in the graph below. Write the sum of the weights of that shortest path (6 points) B 5. Euler and Hamiltonian paths and circuits (10 points) a. Does the following graph contain an Euler circuit? If it does, write down the Euler circuit by listing the vertices in the order that they are visited, starting and ending at vertex A. If it does not, explain why. b. Does the following graph contain an Euler path? If it does, write down the Euler path by listing the vertices in the order that they are visited, starting and ending at a correct vertex. If it does not, explain why. c. Does the following graph (which is slightly different from the first two) have a Hamiltonian circuit? If it does, write down the Hamiltonian circuit by listing the vertices in the order that they are visited, starting and ending at vertex A. If it does not, explain why. A 6. For each of the graphs below (5 points): i. Find A(G) and #(G). ii. CLEARLY label or CLEARLY color each vertex to show a solution based on y(G). o & 7. Color the following map using the smallest number of colors possible. Write that number here: Then, draw a separate planar graph to represent this map. Label your planar graph with the state abbreviations. Note that there are 18 states on this map (10 points). Planar Graph