Question: 1. Let F(x, y, z) = (x cos y)i + (yx)j + (z sin y)k be a vector field on R. Let : R

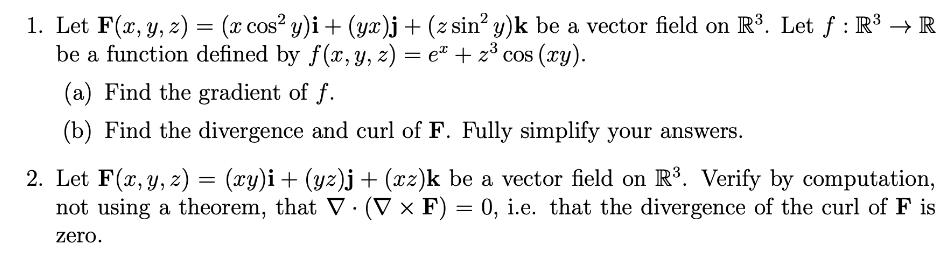
1. Let F(x, y, z) = (x cos y)i + (yx)j +

1. Let F(x, y, z) = (x cos y)i + (yx)j + (z sin y)k be a vector field on R. Let : R R be a function defined by f(x, y, z) = et + z cos (xy). (a) Find the gradient of f. (b) Find the divergence and curl of F. Fully simplify your answers. 2. Let F(x, y, z) = (xy)i + (yz)j + (xz)k be a vector field on R. Verify by computation, not using a theorem, that V (V x F) = 0, i.e. that the divergence of the curl of Fis zero.

Step by Step Solution

★★★★★

3.40 Rating (156 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Par, Inc., is a small manufacturer of golf equipment and supplies. Pars distributor believes a market exists for both a medium-priced golf bag, referred to as a standard model, and a high-priced golf...

Find the gradient of ((x, y, z) = sin(x2 + y2 + z2. Show that the gradient always points directly toward the origin or directly away from the origin.

Find the gradient of the following scalar functions: (a) T = 3 / (x2 + z2), (b) V = xy2 z4|, (c) U =z cos1 + r2), (d) W = e-R sin, (e) S = 4x2e-z + y3,...

Find the gradient of the these scalar fields: (a) U = 4xz2 + 3yz (b) W = 2p(z2 + 1) cos (c) H = r2 cos cos

1. Let f(x, y) = 2x +2y . (a) (8 pts) Write the domain of f using set-builder notation. 4x+ y (b) (18 pts) Sketch the domain of f in the xy-plane. You must justify your sketch with at least four test...

Non-Calculator Lab S-2 1. The graph of the function f, consisting of three line segments and a quarter of a circle, is shown above. Let g be the function defined by g(x) = 2x + Sf(t)dt a. Find the...

35, 49, 53,59 with work please. Thank you 216 CHAPTER 3 Differentiation Rules function. If y = xP/4, then y = x. Use implicit different tion to show that 35-38 Find y" by implicit differentiation. 9...

Let X and Y be independent Poisson random variables with parameters and , respectively. Example 3.12.10 established that X + Y is also Poisson with parameter + . Prove that same result using...

Use resolution to answer the query in Example 3.3.4. Data from Example 3.3.4 This example is taken from the predicate calculus and represents a goal-driven graph search where the goal to be proved...

To substitute in Eq. (14.3), the z-values must be found from Table 14.1 (or Table I). Under the column for "Two-tailed 1 -or," 0.900 (90%) yields z = 1.645 and 0.990 (99%) yields 2.576. Substituting...

6. [-/1 Points] DETAILS HARMATHAP12 9.5.020. Find the indicated derivative. f' ( x) for f(x) = - ( x + 6) (x - 7) x -+ 3 f' ( x) = Need Help? Read It Watch It Submit Answer 7. [0/2 Points] DETAILS...

Physicians RUs is a physician practice in Metropolis. They have 20% of the market in Metropolis and 50% of their patients are insured by UAA. These 10,000 patients average 2.2 visits per year. Their...

Disk A rotates in a horizontal plane about a vertical axis at the constant rate of 0 =15 rad/s. Slider B has a mass of 230 g and moves in a frictionless slot cut in the disk. The slider is attached...

11 Write these decimal numbers in order of size, starting with the smallest. a -8.34,-8.06, -8.28, -8.8 b -1.425, -1.78, -1.03, -1.5

(TOOLS FOR EVALUATING OPERATING DECISIONS) Abu works as an engineer and his wife, Aminah, teaches secondary school. About five years ago they build a 30 x 12 greenhouse to grow tomatoes to sell at a...

Provide examples of some practical applications of Statistical Process Control (SPC) and control charts that you could use to monitor your health, the performance of your car, or the performance of...

A pump delivers water at a steady rate of 1136 L/min. At the upstream of the pump (inlet), the pipe diameter is 9 cm and the pressure is 124 kPa. At the downstream of the pump (outlet), the pipe...

The following events took place during the year for the Boltwood Company. Boltwood manufactures large steel tanks. Boltwood began the year with no inventory. - Incurred 3000 direct labor hours at...

Fill in the Blank Question The manufacturing cycle efficiency is computed by relating the value-added time to the [| (manufacturing cycle} time. (Enter only one word per blank.)

2. Consider the line integral, I = CFdr, where C is defined by the vector function:r (t) = - t2i + t3j + tk, 0t1, and the vector field F (x, y, z) = cos (x) i + sin (y) j + yzkThe value of I is:...

Let C2 be the oriented curve parametriza r(t)= cost V2 ,sint, - cost V2 ), Osts2 n. Let F( x, y, z) = , and let I2=_ F-dr. [Suggestion: Use Stokes' Theorem and the fact that C 2 is the circle in the...

Limits in 3D Worksheet #1. Let f (x, y) = x2+y2 + 3 a) Discuss the continuity of f (x, y) by using the graph below to fill in the blanks (you should study this surface to see if you understand why it...

solve the answers handwritten but please type all the final answers together in the different section after solving. Thanks. 1. [-/1 Points] DETAILS SCALCET9 14.1.004. Let h(x, y) = e (a) Evaluate...

Thanks in advance 1) Let f (x, y) = 4x cos (y). Find the conservative vector field F, which is the gradient of f. Evaluate the line integral of F over the upper half of the unit circle centered at...

854 CHAPTER 15 DIFFERENTIATION IN SEVERAL VARIABLES 9. 20. Jessica and I at 2 oh ; h (x , y ) = -, x = 1/2, y = 1712 paths that make a with velocity va 10. "J : f ( x , y , Z ) = xy - 22, x = rcos0,...