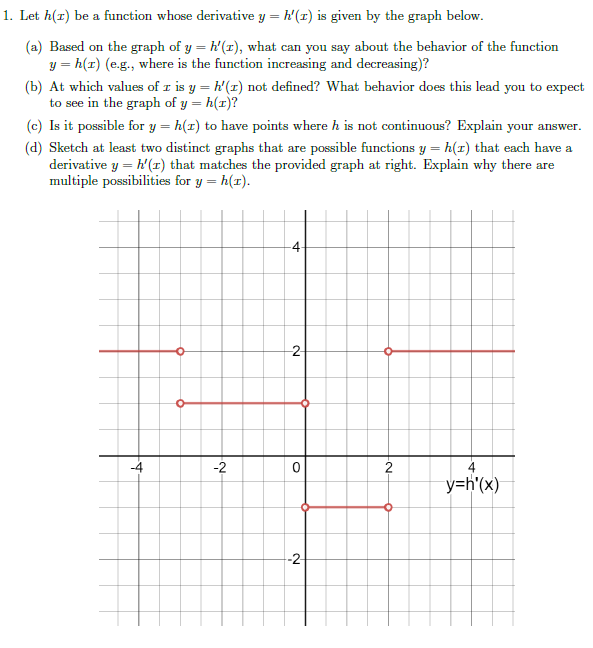
1. Let h(r) be a function whose derivative y = h'(r) is given by the graph below. (a) Based on the graph of y = h'(r), what can you say about the behavior of the function y = h(I) (e.g., where is the function increasing and decreasing)? (b) At which values of r is y = h'(x) not defined? What behavior does this lead you to expect to see in the graph of y = h(I)? (c) Is it possible for y = h(r) to have points where h is not continuous? Explain your answer. (d) Sketch at least two distinct graphs that are possible functions y = h(r) that each have a derivative y = h'(r) that matches the provided graph at right. Explain why there are multiple possibilities for y = h(I). 4- O 2- O- O- -4 -2 0 2 4 y=h'(x) -2