Question: 1) Let x be a continuous random variable that is normally distributed with a mean of 25 and a standard deviation of 5. Find to

to 4 decimal places the probability that * assumes a value a.

between 29 and 35. Probability = b. between 21 and 34. Probability

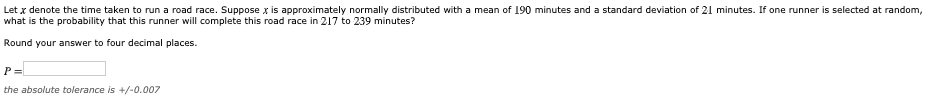
=Let x be a continuous random variable that is normally distributed with

a mean of 24 and a standard deviation of 7. Find the

probability that * assumes a value between 28.7 and 59.0. Use Table

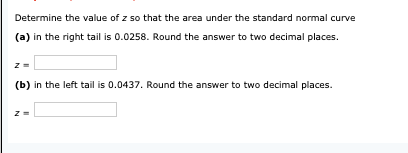
IV in Appendix C to compute the probabilities. Round your answer to

four decimal places. The probability =Let x be a continuous random variable

that is normally distributed with a mean of 65 and a standard

deviation of 15. Find the probability that x assumes a value less

than 46. Round your answer to four decimal places. P the absolute

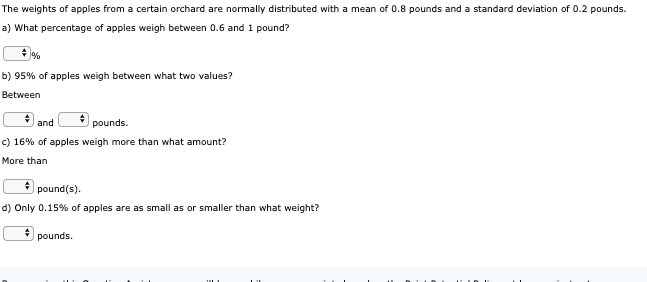
tolerance is +/-0.0035Let x denote the time it takes to run a

road race. Suppose x is approximately normally distributed with a mean of

190 minutes and a standard deviation of 21 minutes. If one runner

is selected at random, what is the probability that this runner will

Let x be a continuous random variable that is normally distributed with a mean of 25 and a standard deviation of 5. Find to 4 decimal places the probability that * assumes a value a. between 29 and 35. Probability = b. between 21 and 34. Probability =Let x be a continuous random variable that is normally distributed with a mean of 24 and a standard deviation of 7. Find the probability that * assumes a value between 28.7 and 59.0. Use Table IV in Appendix C to compute the probabilities. Round your answer to four decimal places. The probability =Let x be a continuous random variable that is normally distributed with a mean of 65 and a standard deviation of 15. Find the probability that x assumes a value less than 46. Round your answer to four decimal places. P the absolute tolerance is +/-0.0035Let x denote the time it takes to run a road race. Suppose x is approximately normally distributed with a mean of 190 minutes and a standard deviation of 21 minutes. If one runner is selected at random, what is the probability that this runner will complete this road race in less than 191 minutes? Round your answer to four decimal places. P = the absolute tolerance is +/-0.0035 By accessing this Question Assistance, you will learn while you earn points based on the Point Potential Policy set by your instructor.Let x denote the time taken to run a road race. Suppose x is approximately normally distributed with a mean of 190 minutes and a standard deviation of 21 minutes. If one runner is selected at random, what is the probability that this runner will complete this road race in 217 to 239 minutes? Round your answer to four decimal places. P = the absolute tolerance is +/-0.007A construction zone on a highway has a posted speed limit of 35 miles per hour. The speeds of vehicles passing through this construction zone are normally distributed with a mean of 42:02 miles per hour and a standard deviation of 3 miles per hour. Find the percentage of vehicles passing through this construction zone that are exceeding the posted speed limit. Round your answer to two decimal places. The percentage is the absolute tolerance is +/-0.3Find the value of 237) the absolute tolerance is +/-0.0001

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

8th-ed Chap 02, Sec 2.2, Problem 018 The accompanying table lists the 2010 median household incomes, rounded to the nearest dollar, for all 50 states and the District of Columbia. 2010 Median...

Solutions only no work needs to be shown for the 4 questions. 1.Find the area under the standard normal curve betweenz=-1.67 and z=2.44 . Round your answer to four decimal places. A= 2.Obtain the...

View Policies Current Attempt in Progress Let x be a continuous random variable that is normally distributed with a mean of 108.9 and a standard deviation of 15.2. Find the probability that x assumes...

Let x be a continuous random variable that is normally distributed with a mean of 61 and a standard deviation of 15. Find to 4 decimal places the probability that x assumes a value a. less than 36 b....

Question 12 of 35 Current Attempt in Progress Let x be a continuous random variable that is normally distributed with a mean of 74 and a standard deviation of 15. Find to 4 decimal places the...

Let x be a continuous random variable that is normally distributed with a mean of 47 and a standard deviation of 12 . Find the probability that x assumes a value less than 54 . Round your answer to...

Let x be a continuous random variable that is normally distributed with a mean of 25 and a standard deviation of 6. Find the probability that x assumes a value a. between 29 and 36 b. between 22 and...

6.33 Let x be a continuous random variable that is normally distributed with a mean of 25 and a standard deviation of 6. Find the probability that x assumes a value a. between 29 and 36 b. between 22...

Let x be a continuous random variable that is normally distributed with a mean of 23 and a standard deviation of 6 (a) Write a cumulative probability statement for the area under the normal curve to...

Let x be a continuous random variable that is normally distributed with a mean of 27 and a standard deviation of 6. Round answers to two decimal places. (a) Standardize the variable value x = 30.0 z...

How can systems that implement the principle of least privilege still have protection failures that lead to security violations?

Suzette Companys liabilities as reported on the June 30, 2014, balance sheet are shown below, along with its statement of changes in equity. Accounts payable...

Hostess and Kodak recently filed for bankruptcy protection in an attempt to restructure their debts. One could assume that both of these companies experienced too much risk: A . financial B ....

Shoe Corporation and Sock, Inc. exchanged two pieces of property in a qualifying like-kind exchange. Stuff That Stuff That Shoe Exchanged Sock Exchanged Original purchase 4/1/03 11/15/02 Adjusted...