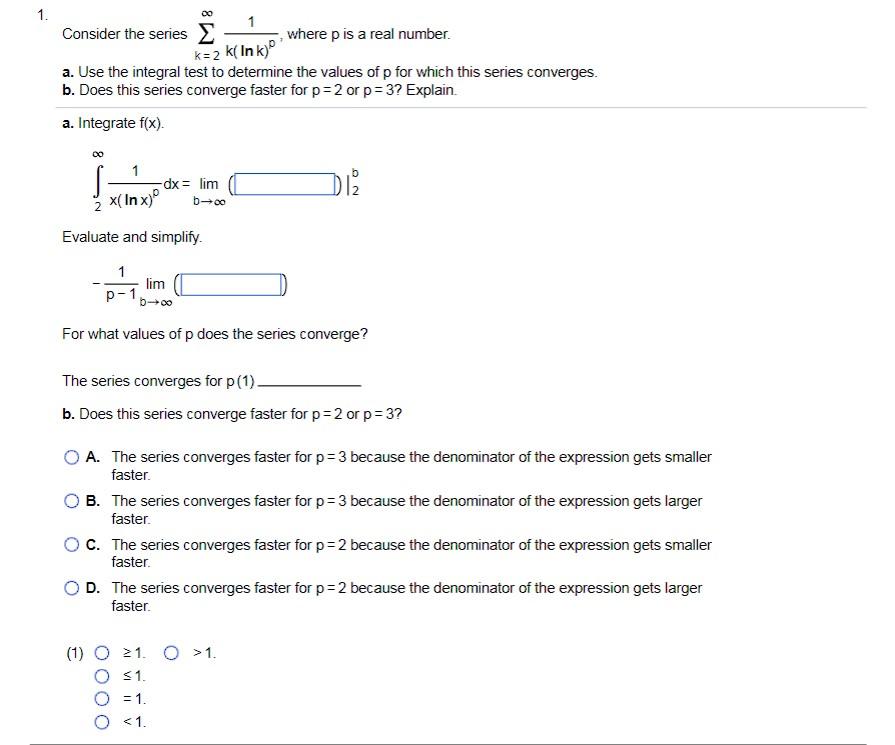
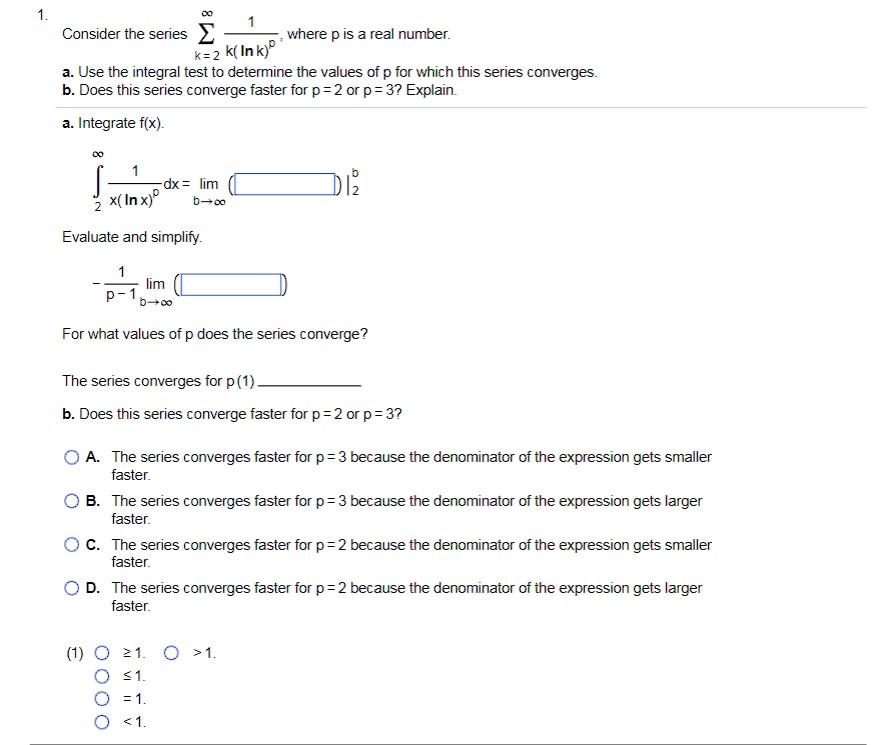
1. M : Consider the series , where p is a real number. k=2 k( Ink) a. Use the integral test to determine the values of p for which this series converges. b. Does this series converge faster for p = 2 or p = 3? Explain. a. Integrate f(x). dx = lim No x( In x) b -+cc Evaluate and simplify. lim p - b-+co For what values of p does the series converge? The series converges for p (1) b. Does this series converge faster for p = 2 or p = 3? O A. The series converges faster for p = 3 because the denominator of the expression gets smaller faster. O B. The series converges faster for p = 3 because the denominator of the expression gets larger faster. O C. The series converges faster for p = 2 because the denominator of the expression gets smaller faster. O D. The series converges faster for p = 2 because the denominator of the expression gets larger faster. (1) O 21. 0 > 1. O $1. O = 1. O =1