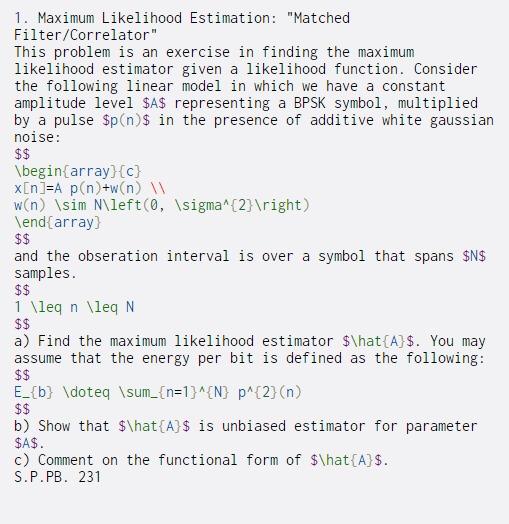
1. Maximum Likelihood Estimation: "Matched Filter/Correlator" This problem is an exercise in finding the maximum likelihood estimator given a likelihood function. Consider the following linear model in which we have a constant amplitude level $A$ representing a BPSK symbol, multiplied by a pulse $p(n)$ in the presence of additive white gaussian noise: $$ \begin{array}{c} x[n]=A p(n)+w(n) W w(n) \sim N\left(0, \sigma^{2} ight) \end{array} $$ and the obseration interval is over a symbol that spans $N$ samples. $$ 1 \leq n \leq N $$ a) Find the maximum likelihood estimator $\hat{A}$. You may assume that the energy per bit is defined as the following: $$ E_{b} \doteq \sum_{n=1}^{N} p^{2}(n) $$ b) Show that $\hat{A}$ is unbiased estimator for parameter $A$. c) Comment on the functional form of $\hat{A}$. S.P.PB. 231