1. Naive LU Decomposition

Starting with your functioning Gauss Elimination code from last assignment, modify it to keep the factors in the same matrix that it is passed.

Last assignment code:

clear

A=input('Enter Matrix A:')

Ao=A;

B=input('Enter Solution Vector B:')

Bo=B;

n=size(A,1);

for k=1:n-1

for i=k+1:n

factor=A(i,k)/A(k,k);

for j=k+1:n

A(i,j)=A(i,j)-factor*A(k,j);

end

B(i)=B(i)-factor*B(k);

end

end

X(n)=B(n)/A(n,n);

for i=n-1:-1:1

sum=0;

for j=i+1:n

sum=sum+A(i,j)*X(j);

end

X(i)=(B(i)-sum)/A(i,i);

end

Solution=X.'

You of course will not modify the b-vector. Have this function return the L and U matrices in a single matrix. You do not need to create separate L and U matrices. Note that Matlab's lu() will also do this, but may perform row swapping (so you need to be careful with direct comparisons).

Decompose the given 3x3 A matrix (above), and confirm your correct decomposition by computing LU = A. Provide a command prompt printout.

Then write a solver function and use the LU solution technique to solve the (above) 3x3 system. Again, show this work with a printout of the command prompt window. Specifically, the technique first solves L d = b for d by back substitution, then U x = d for x by forward substitution.

2. Solve A MUCH Larger System (In MATLAB only)

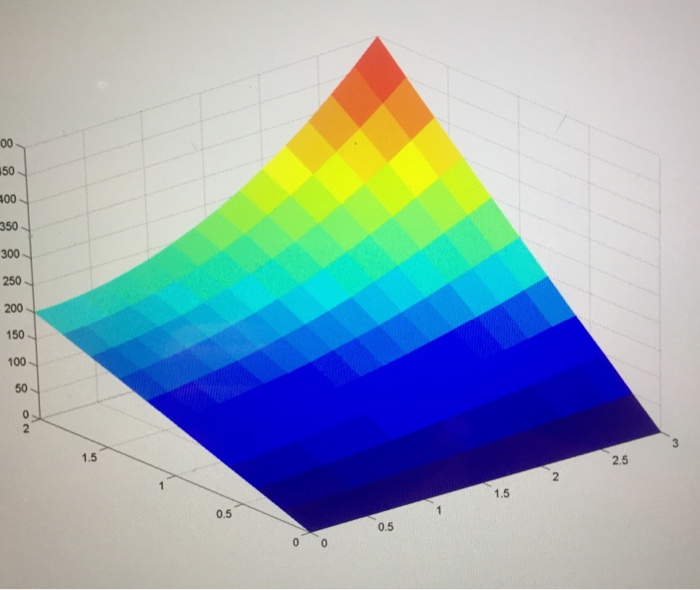
Solving partial differential equations (PDEs) numerically gives rise to large matrix systems. Download ConcentrationGradient.mat which contains the A and b components (named Am and bv) of a linear system composed from numerically discretizing the PDE describing a chemical concentration in a two-dimensional region given specific boundary concentrations. The steady state concentration appears so:

Concentration_Setup.bmp

You are to use one of your two hand-written matrix solution techniques to solve for this concentration map. Use the following steps:

Load ConcentrationGradient.mat - it contains four variables: Am (the A matrix), bv (the right hand side b vector), and Nx & Ny, variables that define the grid size in the x and y directions.

Solve the system [Am c = bv] using one of your two techniques

Visualize the resulting gradient:

First, reshape the resulting solution into a matrix of the appropriate shape using the command cXY = reshape(c, Nx, Ny).

Then visualize the solution with the command surf(cXY). Note that your solution does not contain the boundary concentrations, so it won't quite have the same extent as the solution above.

Provide your plot as the answer to this problem.

350 300 250 200 150 100 50 0.5