$1$ne rollowing function simulates a "random walk," using a matrix to store the random walk as it progresses. To begin with all elements are initialized to $1.$ Then, the "middle" element is chosen to be the starting point for the random walk; a $2$ is placed in that element. $($Note: these numbers will eventually represent colors.$)$ Then, from this starting point another element next to the current one is chosen randomly and the color stored in that element is incremented; this repeats until one of the edges of the matrix is reached. Every time an element is chosen for the next element, it is done randomly by either adding or subtracting one to$/$from each coordinate $(x$ and $y),$ or leaving it alone. The resulting matrix that is returned is an $n$ by $n$ matrix.

function walkmat $=$ ranwalk $(n)$

walkmat $=$ ones $(n)$;

$x=flr(\frac{n}{2})$;

$y=flr(\frac{n}{2})$;

color $=2$;

walkmat $(x,x)=$ color;

while $x=1$ && $x=n$ && $y=1$ && $y=n$

$x=x+$randi$(\left[\begin{array}{cc}-1& 1\end{array}\right])$;

$y=y+$ randi $(\left[\begin{array}{cc}-1& 1\end{array}\right])$;

color $=$ color $+1$ ;

walkmat $(x,y)=$mod$(color,65)$;

end

end

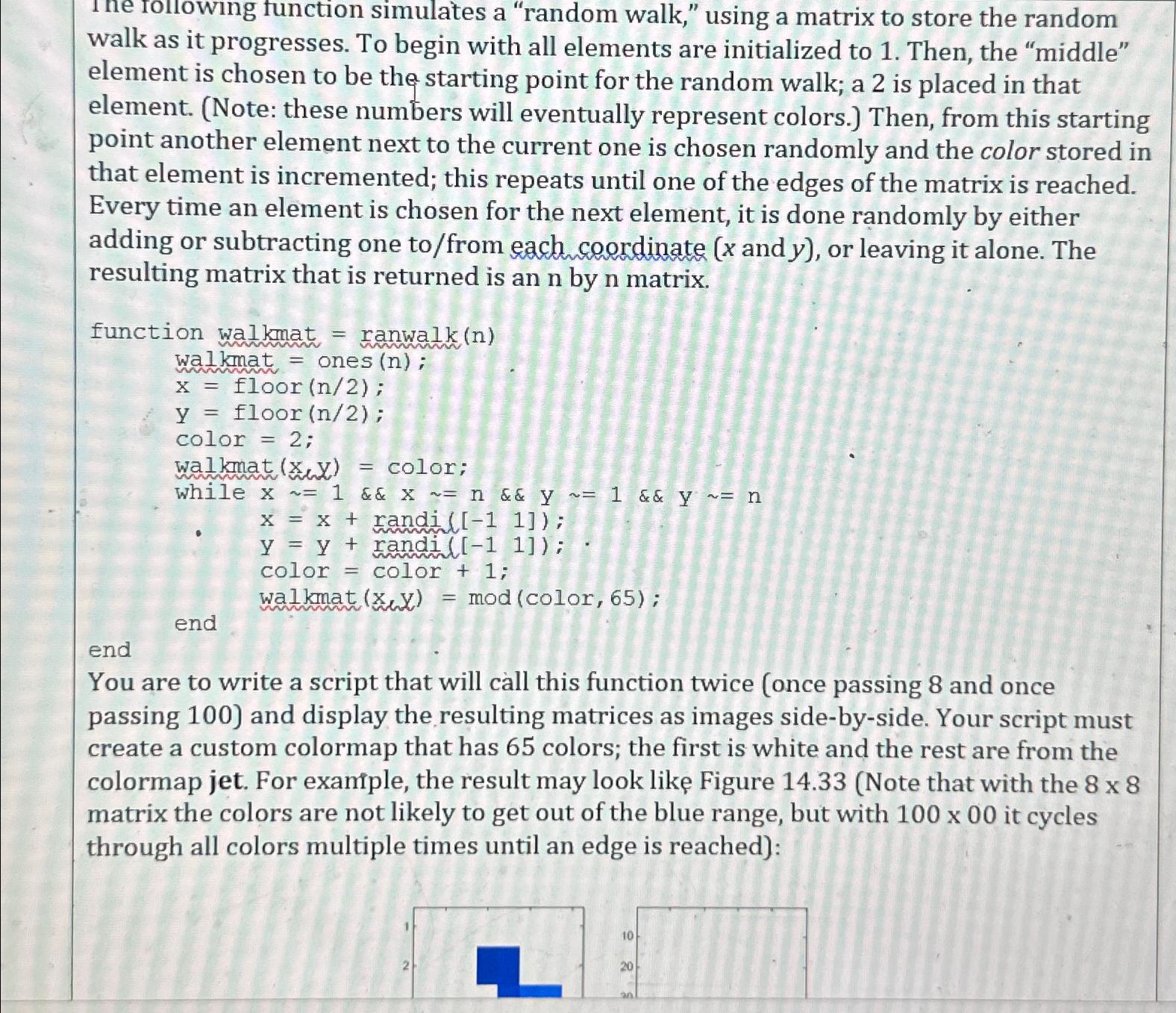
You are to write a script that will call this function twice $($once passing $8$ and once passing $100)$ and display the resulting matrices as images side$-$by$-$side. Your script must create a custom colormap that has $65$ colors; the first is white and the rest are from the colormap jet. For example, the result may look like Figure $14\mathrm{.}33($Note that with the $88$ matrix the colors are not likely to get out of the blue range, but with $10000$ it cycles through all colors multiple times until an edge is reached$)$: