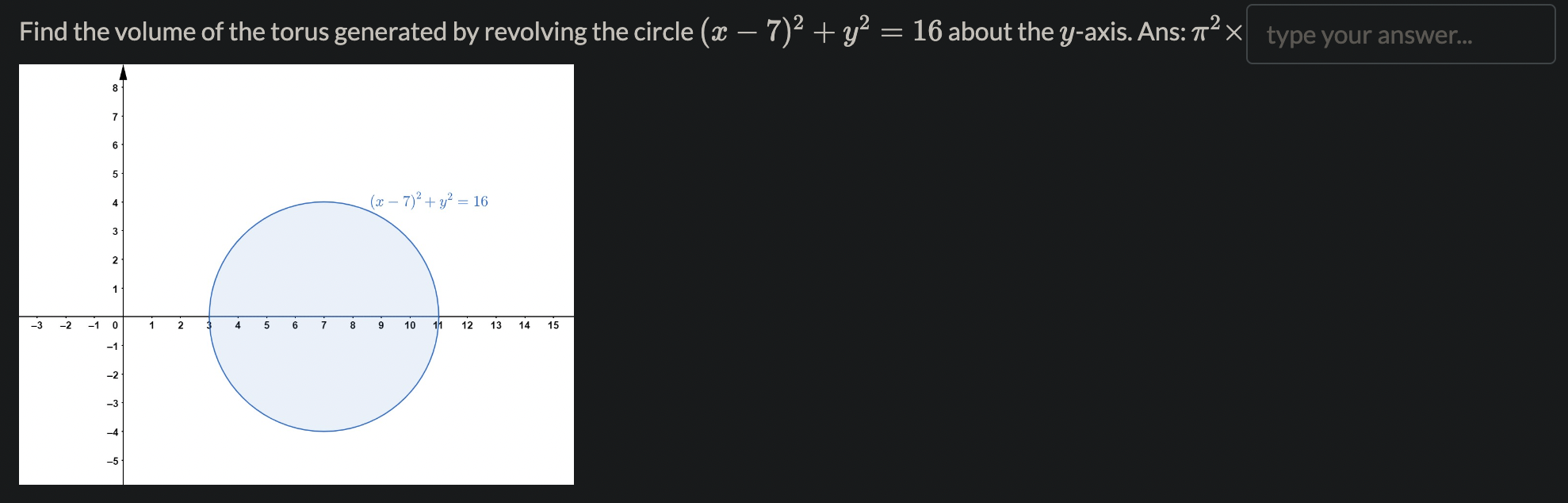
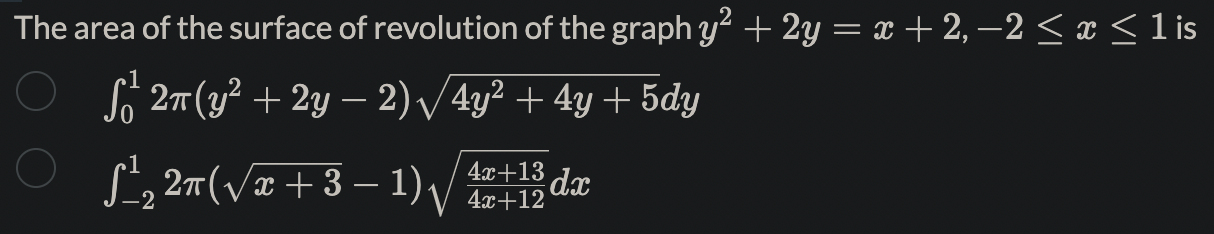
1. (Options for blanks: Disk method, Shell method, Slice method, Washer method)

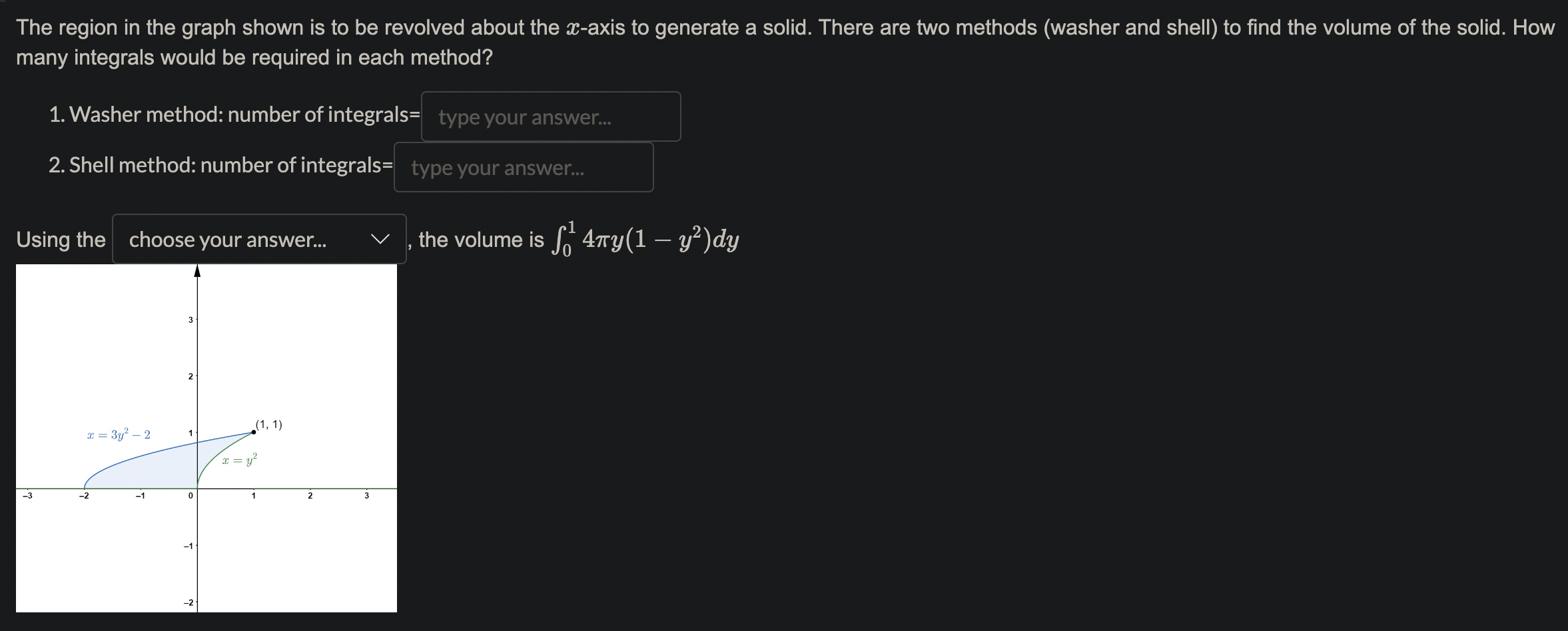
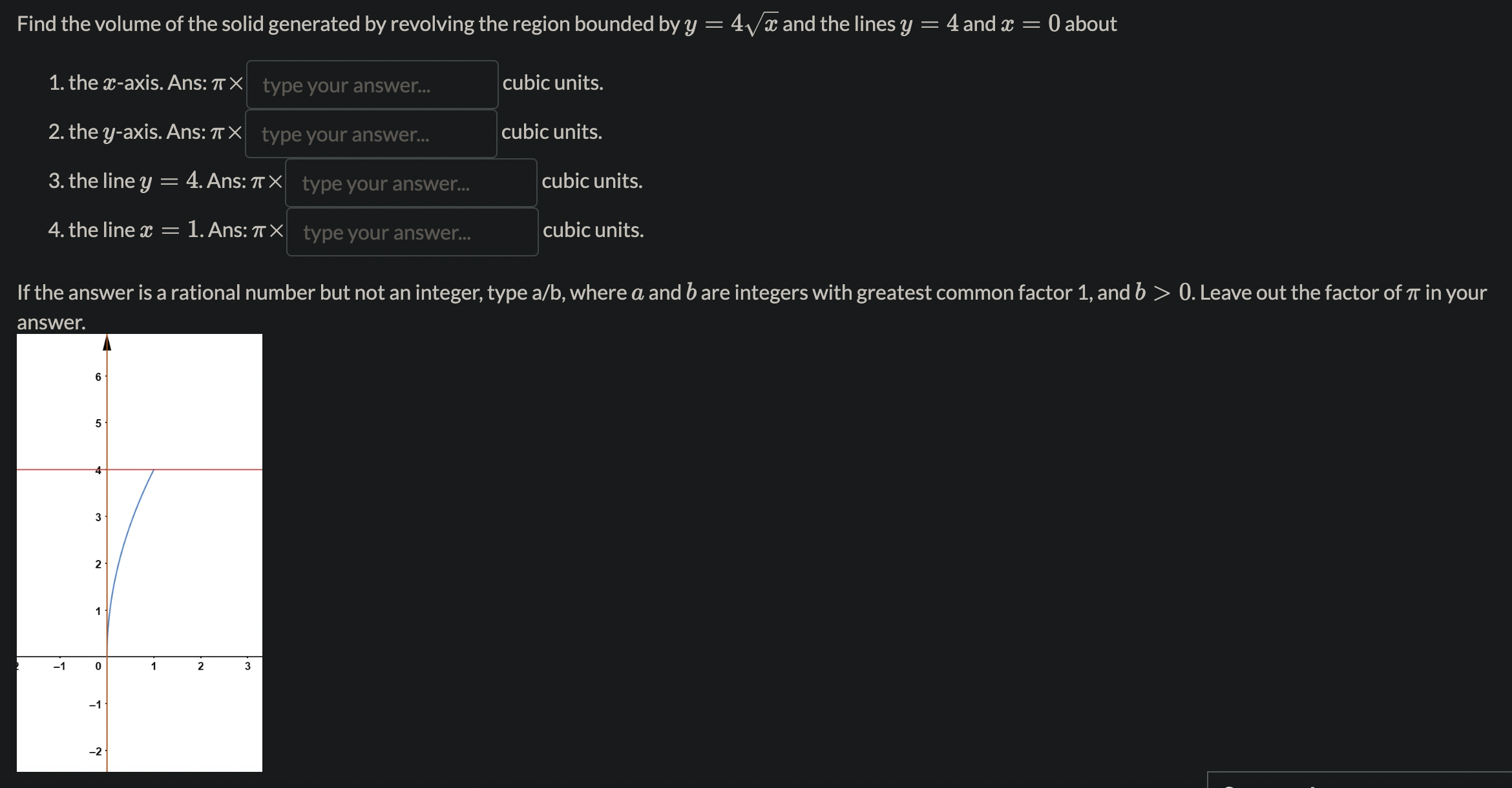
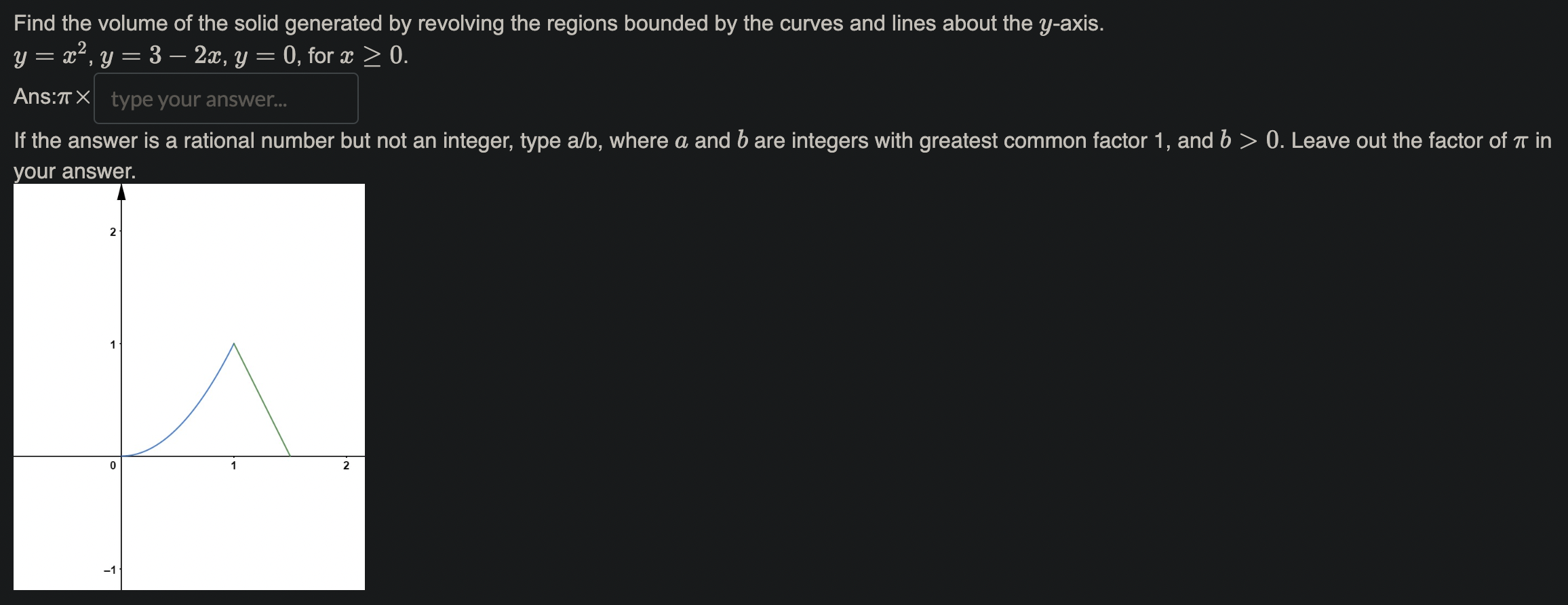
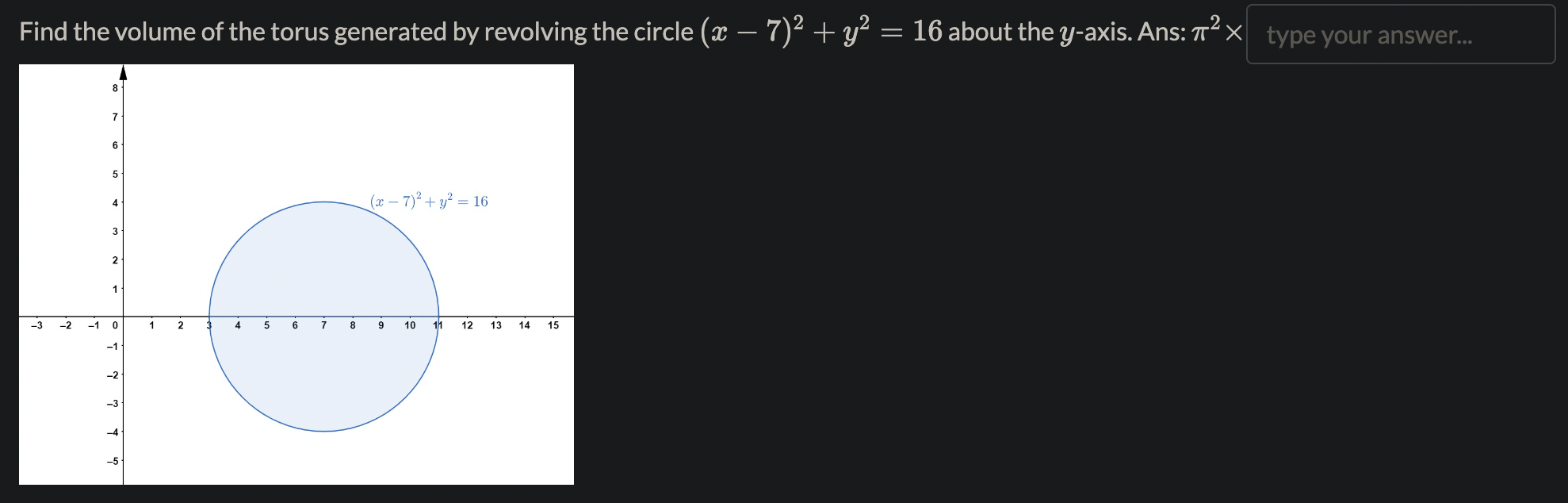
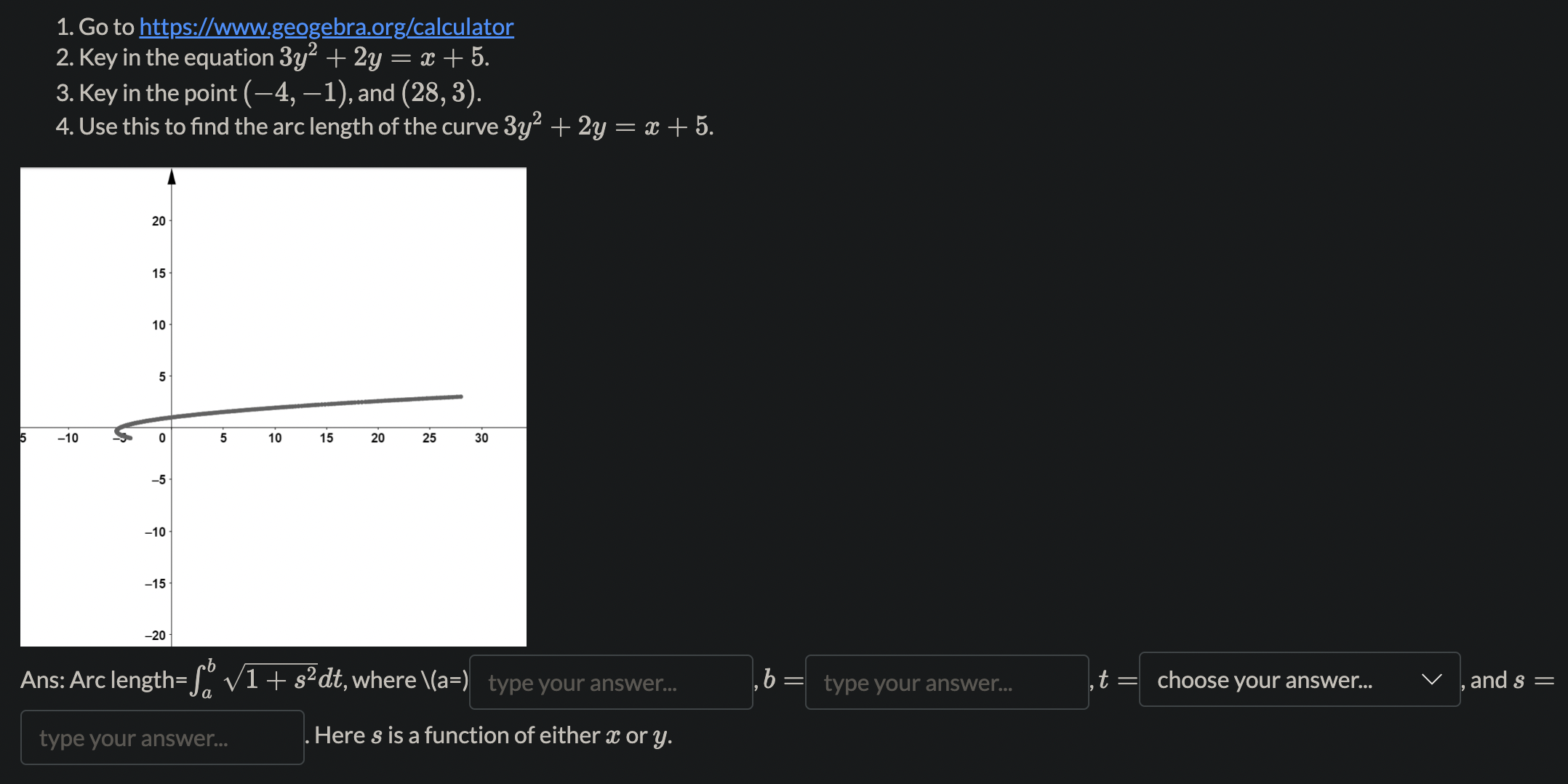
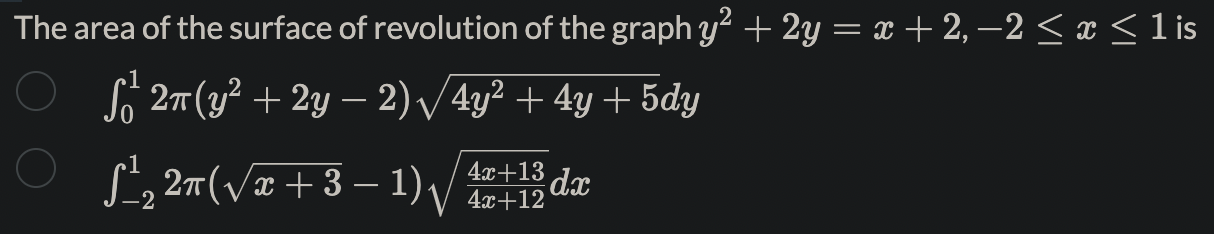
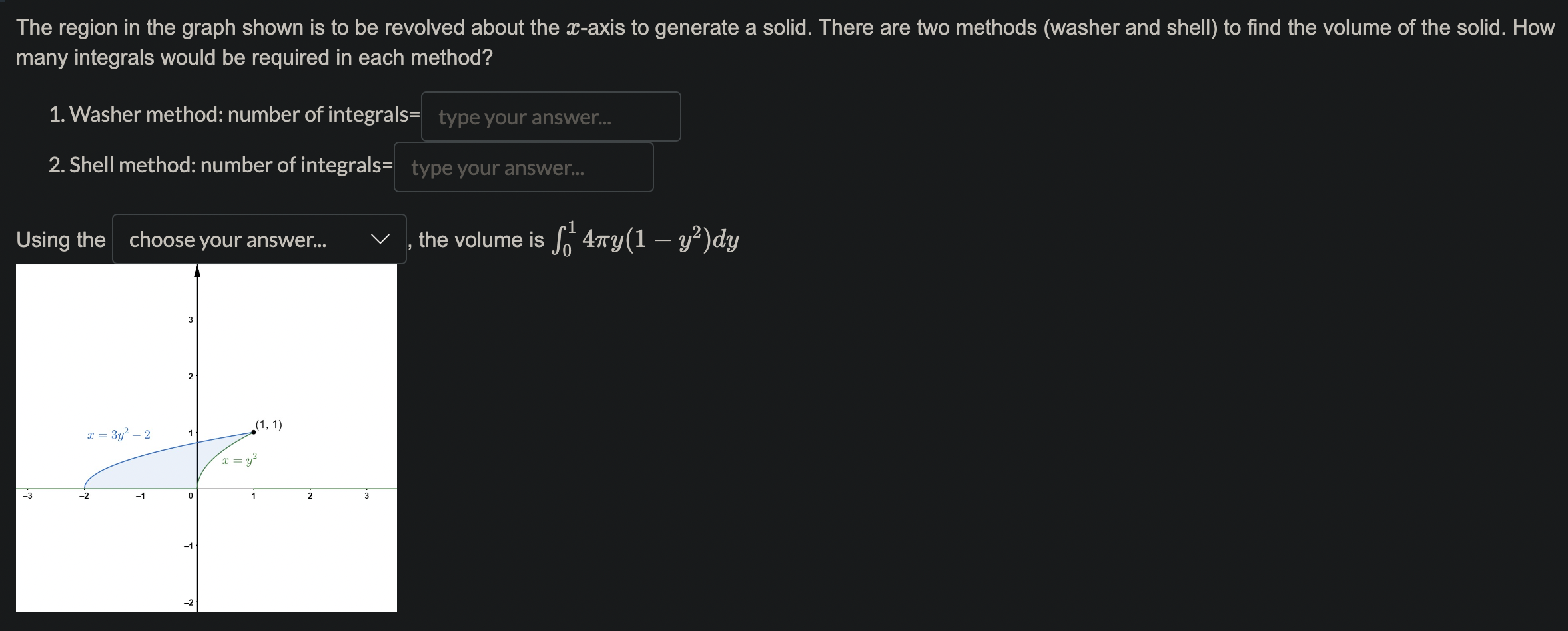
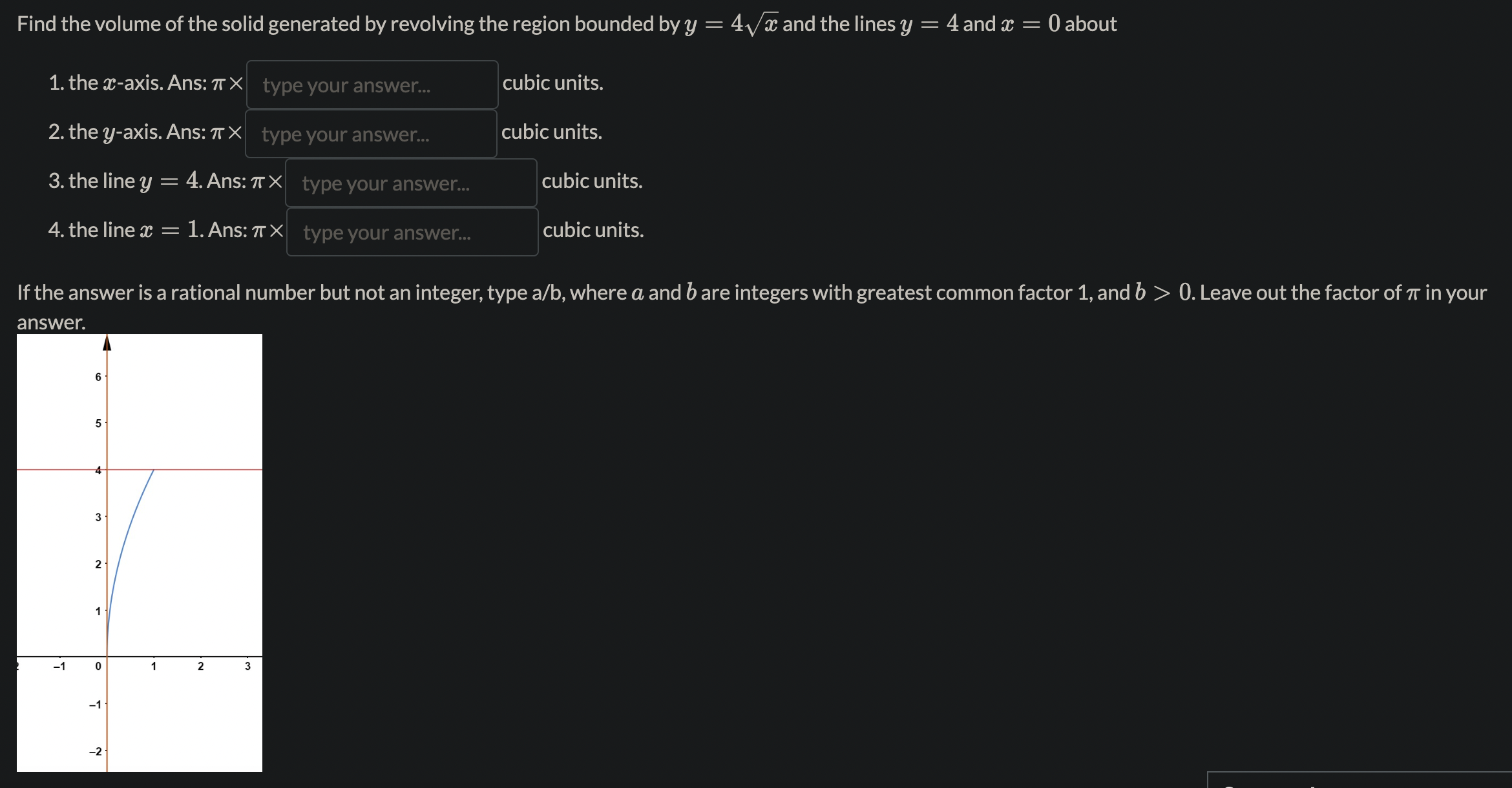
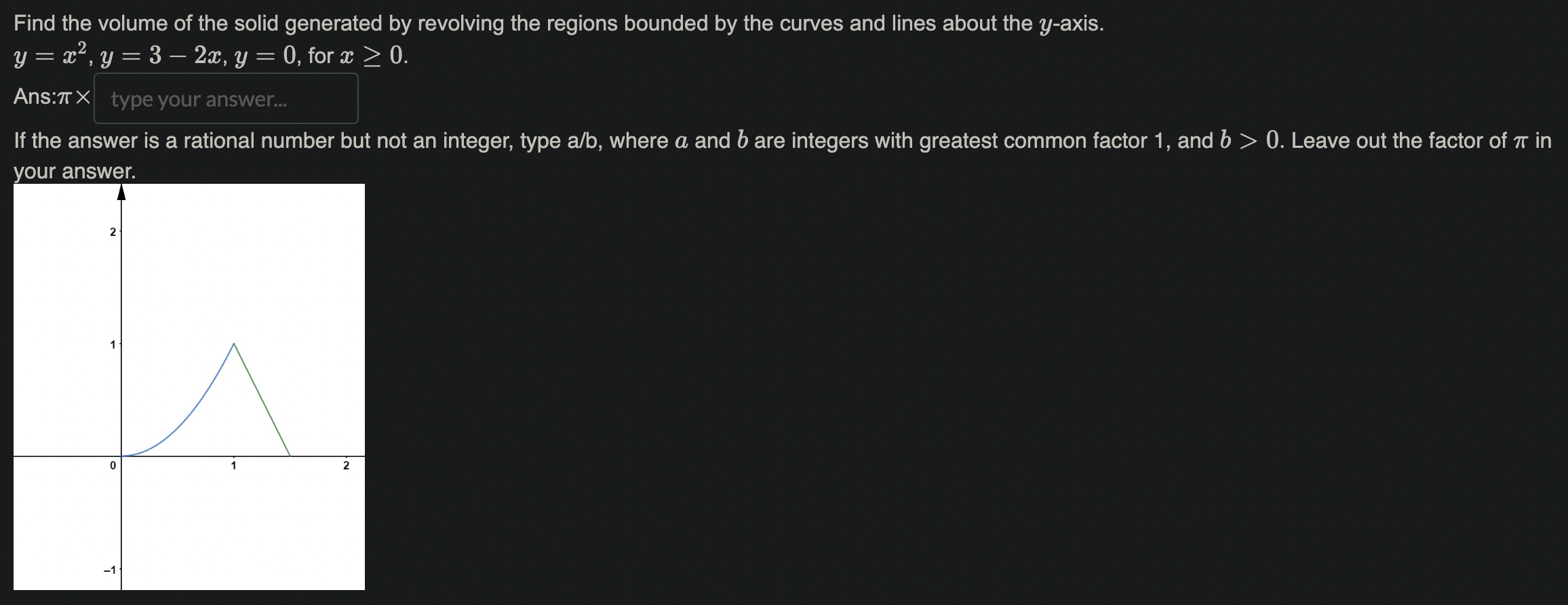
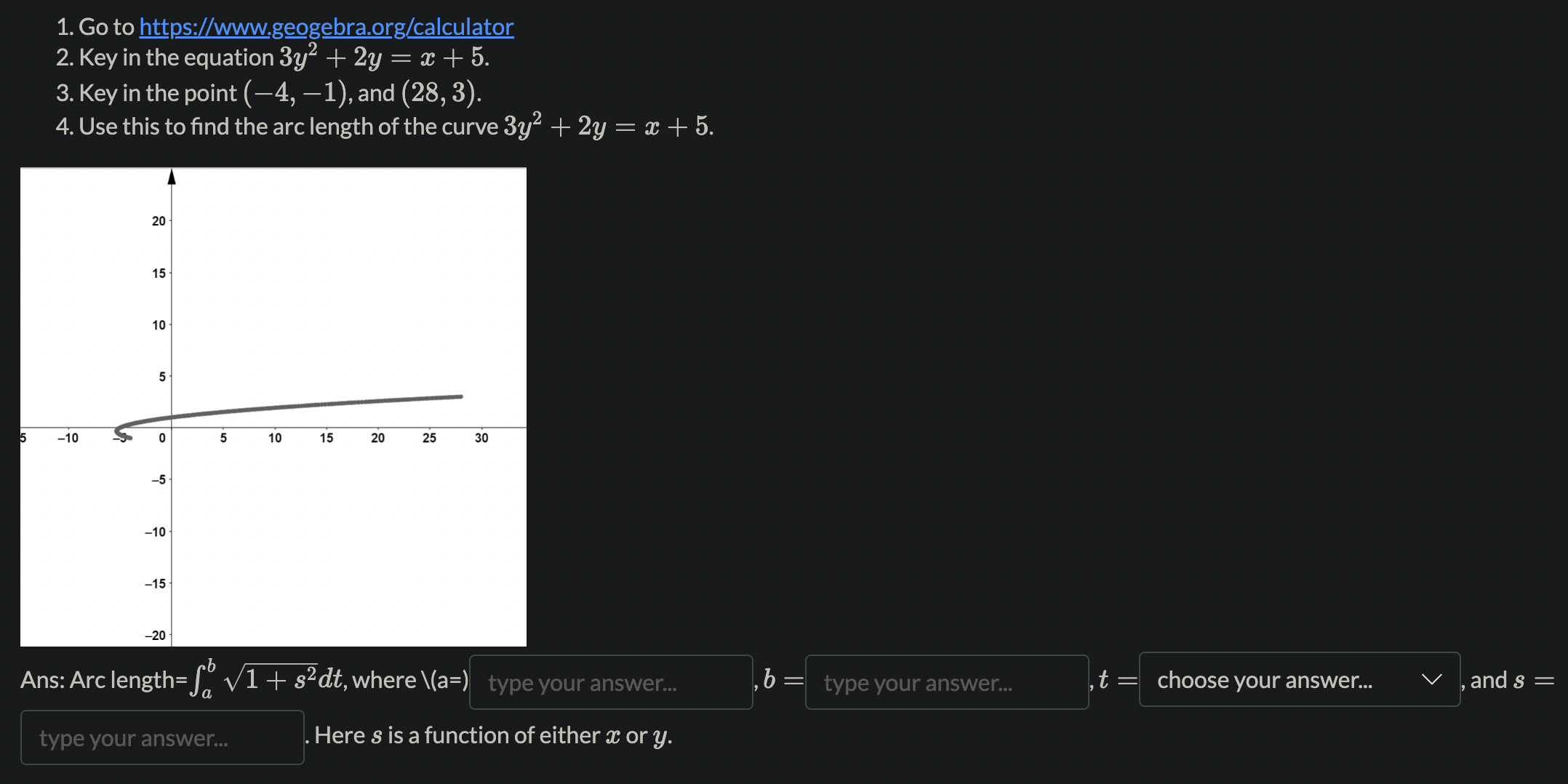
Name the methods used in finding the volumes. 1. So A(x) da choose your answer.. 2. So T(r(x) )2da choose your answer. 3. So T [(R(x))2 - (r(x) )2 da choose your answer., V 4. Jo 2raf (x) dx choose your answer...Consider the following solid. It lies between planes perpendicular to the x-axis at a = -1 and = 1. The cross-sections perpendicular to the x-axis are circular disks whose diameters run from the parabola y = x2 to the parabola y = 2 - x2. Which of the following is the volume of the solid? To aid in the visualization, you may click on the link: 3DGeogebra and follow the instructions. 1. Input eq1: (y-1)^2+z^2=1, enter 2. Input eq2: x=0, enter 3. Input c: IntersectPath(eq2,eq1), enter 4. Click on the colored circle beside eq1 and eq2 to hide them. 5. Input y=x^2, enter 6. Input y=2-x^2, enter 7. Input x=-1, enter 8. inout x=1, enter 2 521-x2da 26 1-x2da T (1-x2)2da T. So(1 - 12)2daThe region in the graph shown is to be revolved about the m-axis to generate a solid. There are two methods (washer and shell) to nd the volume of the solid. How many integrals would be required in each method? 1. Washer method: number of integrals= 2. Shell method: number of integrals: Using the choose your answer... V , the volume is fol 47ry(1 * y2)dy Find the volume of the solid generated by revolving the region bounded by y : 4V Eand the lines y : 4 and m : 0 about 1. the $axis. Ans: 7r > 0. Leave out the factor of 7r in your a nswer. Find the volume of the solid generated by revolving the regions bounded by the curves and lines about the y-axis. y=x2,y=32m,y=0,for$ 20. Ans:7r X If the answer is a rational number but not an integer, type a/b, where a and b are integers with greatest common factor 1, and b > 0. Leave out the factor of 71' in your answer. Find the volume of the torus generated by revolving the circle (a: 7)2 + y2 = 16 about the y-axis. Ans: 7r2 X 12 13 1a 15 1. Go to https://www.geogebra.org/calculator 2. Key in the equation 3y2 + 2y = x + 5. 3. Key in the point (-4, -1), and (28, 3). 4. Use this to find the arc length of the curve 3y2 + 2y = x + 5. 20 15 10 5 5 -10 0 5 10 15 20 25 30 -5 -10 -15 -20 Ans: Arc length= S V1 + s2dt, where \\(a=) type your answer.. b type your answer.. t = choose your answer... V and s = type your answer.. Here s is a function of either x or y.l c 1_Td daz,where a = b Using the arc length formula for compute the circumference of the unit circle, we have C = 4 fa \\'J ,6: d: Hint: The answers are integers. Recall that the graph of the unit circle is given by m2 + y2 = 1. The area of the surface of revolution of the graph y~ + 2y = x + 2, -2 0. Leave out the factor of 71' in your