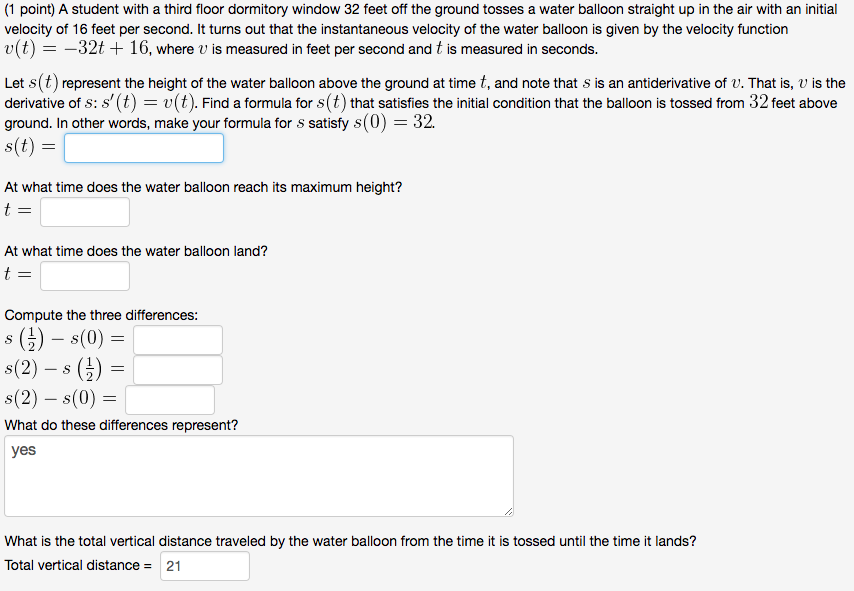
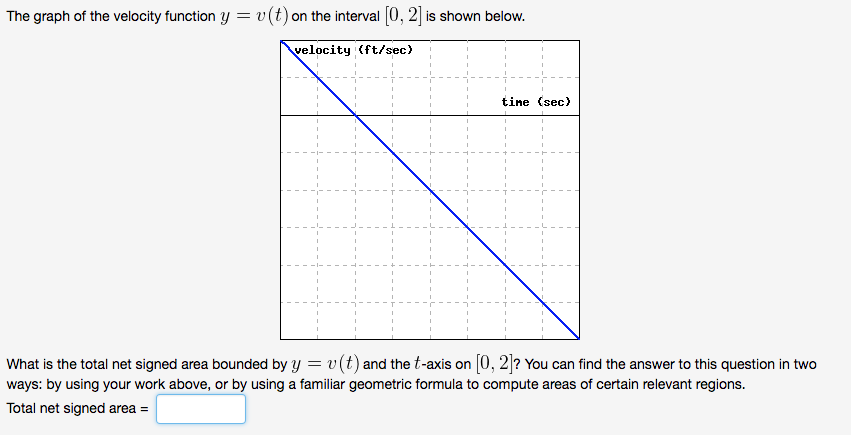
[1 point} A student with a third oor dormitory window 32 feet off the ground tosses a water balloon straight up in the air with an initial velocity of 15 feet per second. It tums out that the Instantaneous velocity of the water balloon is given by the velocit},f function t) I 32t -l- 15, where \"U ls measured In feet per second and 15 Is measured In seconds. Let SH) represent the height of the water balloon above the ground at time t. and note that 5 is an antiderivative of \"U. That is. 1:} Is the derivative of 5: 5' (it) 2 12 (it). Find a formula for 5 (t) that satises the initial conditlon that the balloon is tossed from 32 feet above ground. In other words. mal-ce your formula for S satisfy 5(0) = 32. at) = E At what time does the 1titrater balloon reach its maximum height? it: At what time does the water balloon land? it : Compute the three dlfferenoes: sit) 5(0) = 5(2) 5 (a = 5(2) s( = What do these differences represent? yes A I.nlhat is the total vertical distance traveled by the water balloon from the time It is tossed until the time It lands? Total vertical distance = 21 The graph of the veloolty funotlon y = v (t) on the Interval [I], 2] Is shown below. ____J____L____ ____J____L____L___ ____W'"'T____F"'W____T_"' can find the answer to this question In two LI What is the total net signed area hounded by y = \"U (t) and the t-axis on [I], 2]? Yo ways: by using your work above, or by ualng a famillar geometric formula to compute areas of certain relevant reglona. Total net signed area = C]