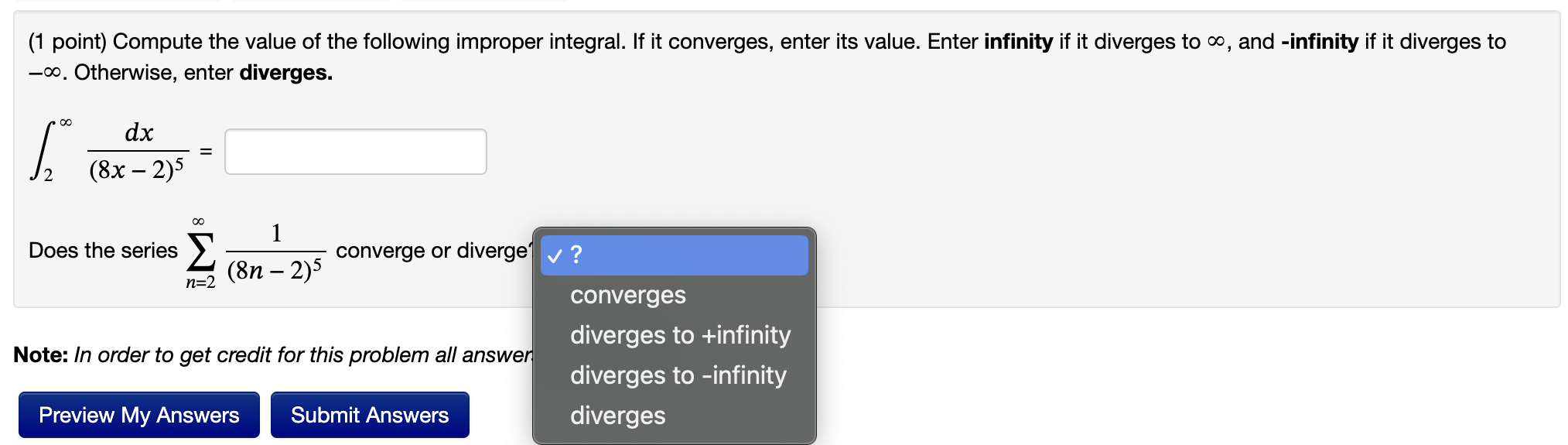
(1 point) Compute the partial sums S2, S4, and S6. 3 3+ + 22 S = S4= S6 = 3 3 + 32 (1 point) Let 9n an = 2n+5' For the following answer blanks, decide whether the given sequence or series is convergent or divergent. If convergent, enter the limit (for a sequence) or the sum (for a series). If divergent, enter 'infinity' if it diverges to *, '-infinity' if it diverges to - or 'DNE' otherwise. (a) The series 9n 2n+5 infinity n=1 (b) The sequence { 9n 2n+5 (1 point) The following series are geometric series or a sum of two geometric series. Determine whether each series converges or not. For the series which converge, enter the sum of the series. For the series which diverges enter "DIV" (without quotes). 9n (2) = DIV 8n 3" n=2 3" (c) 92n+1 n=0 8" (d) () 9n 7" DIV 71+4 8" + 3" 9n 8W WWI WI WI WI 00 (1 point) Determine whether the series converges, and if so find its sum. IM 8 k=1 2k+2 7k-1 (Enter DNE if the sum does not exist.) (1 point) Consider the following series. Answer the following questions. 1. Find the values of x for which the series converges. Answer (in interval notation): 2. Find the sum of the series for those values of x. Sum: 8 WI n=0 (x+4)" 2" (1 point) Calculate S3, S4, and S5 and then find the sum for the telescoping series S = 00 3-(--) n+2 where S is the partial sum using the first k values of n. S3 = S4= S5 = S = (1 point) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to co, and -infinity if it diverges to -co, Otherwise, enter diverges. dx (8x-2)5 Does the series 1 converge or diverge ? (8n-2)5 n=2 converges Note: In order to get credit for this problem all answer Preview My Answers Submit Answers diverges to +infinity diverges to -infinity diverges (1 point) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to , and -infinity if it diverges to -. Otherwise, enter diverges. 2 dx x + 1 Does the series 2 n + 1 converge or diverge? ? n=1