Question: (1 point) Consider the curve described by the parametric equations: X= 7 - + 41 + 2 (a) Find the values of t where the

where the curve intersects itself: f=t (b) Find the area of the

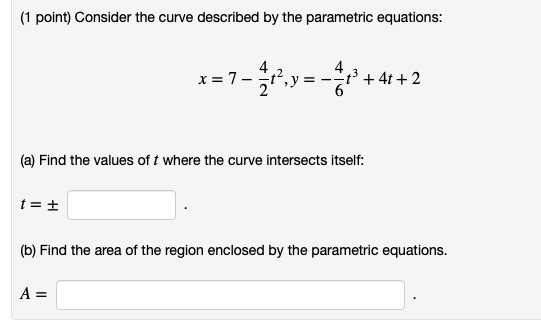
(1 point) Consider the curve described by the parametric equations: X= 7 - + 41 + 2 (a) Find the values of t where the curve intersects itself: f=t (b) Find the area of the region enclosed by the parametric equations. A =(1 point) Find the area of the region enclosed by the parametric equations: x =1' - 3t,y = 812, -V/3 5+s v3 A =(1 point) Find the area of the surface obtained by rotating the following curve about the x- axis. x = 5t - +', y = 512, 06151 Surface Area =

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Please answer the Questions correctly. Please type only the answers. Thank you. 2. [OH Points] DETAILS PREVIOUS ANSWERS SCALCET910.2.038'MI. 5/100 Submissions Used MY NOTES ASK YOUR TEACHER PRACTICE...

nwindin . S trin . In this problem, we will be thinking about a parametric curve and imagining a string unwound From that curve. We are trying to think about the path traced out by the end oF the...

Entered Answer Preview Result 3.9428 3.9428 incorrect 15.989 15.989 incorrect At least one of the answers above is NOT correct. Consider the curve described by the parametric equations: C = 5- =- -+...

Mark as Complete V Ou=_V5 2V5 5 5 Ous-V3 2V3 20. Which of the following is a point on the plane curve defined by the parametric equations? x =3t y =1&2 +12 +2 (1 point) O (-1, 0) O (-3,-28) O (-1, 8)...

15. [-/0.12 Points] DETAILS SCALCET9 10.2.055. 0/100 Submissions Used MY NOTES ASK YOUR TEACHER Find the distance traveled by a particle with position (x, y) as t varies in the given time interval. x...

help!!! . Find the exact surface area of the surface obtained by rotating the curve y =1- .r2 where 0 S x S 1 about the y-axis. Suppose a two dimensional plate with uniform density occupies the...

Please Answer The Following Questions, show all work please! 1. (4 pts. each) Consider a curve given by the parametric equations: = t+ Int y = t- Int (a) Find an equation of the line tangent to the...

vo Designing Interactive Applications Distinguish the phrases wishes evaluation and requirements analysis. Provide an example to illustrate the distinction. [3 marks] What is a robust requirement?...

7. Given x = 5cost and y = 4sint, find in terms of t a) dy dx [4] b) d2 y dx2 [5] 8. A curve is defined by parametric equations x = t2 + t - 1 and y = 2t2 - t + 2 for all t i. Show that A(-1,5) lies...

Find the exact length of the curve described by the parametric equations. X=5+3t2, y=1+2t3, 05:55 :x Find the surface area generated by rotating the given curve about the y-axis. x = 6t2, y = 4+3,...

3. Two parallel metal plates have a potential difference of 2000V applied across them as shown. A particle of mass 4 x 10-10 kg and carrying a charge Q = +9 x 10-9 C is placed at the positive pole...

answers you use your cale Suppose that the spot price of a Canadian dollar is U.S. $0.93 and that the exchange rate has a 1. volatility of 5% per year. Risk-free interest rates are 6% in the U.S. and...

on Corner writes 4 4 checks a day for an average amount of $ 5 5 3 each. These checks generally clear the bank 3 days after they are written. In on , the firm generally receives 8 1 checks with an...

Gardner Company expects sales for October of $245,000. Experience suggests that 45% of sales are for cash and 55% are on credit. The company collects 50% of its credit sales in the month of sale and...