Question: (1 point) Consider the function / (2) = 7+e (a) f(x) . (0) f is increasing for I E (c) f is decreasing for I

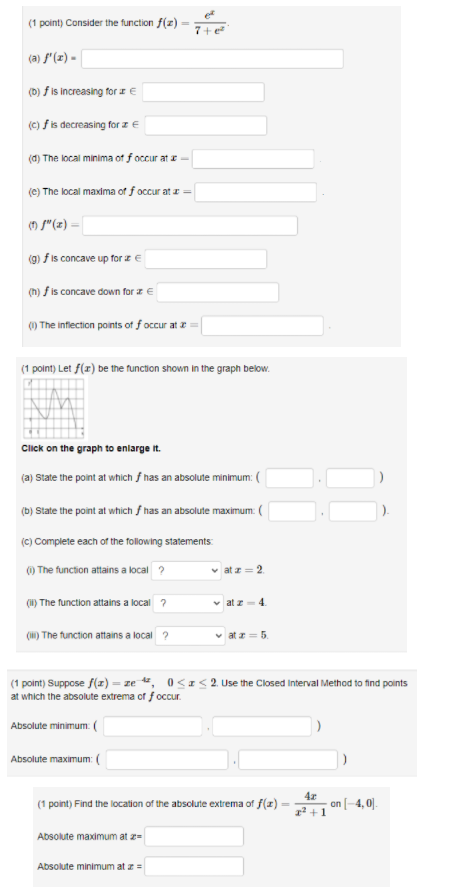
(1 point) Consider the function / (2) = 7+e (a) f(x) . (0) f is increasing for I E (c) f is decreasing for I E (d) The local minima of f occur at c - (e) The local maxima of f occur at = = ( f(=) = (9) f is concave up for I E (h) f is concave down for = e (1) The inflection points of f occur at = (1 point) Let f(r) be the function shown in the graph below. Click on the graph to enlarge it. (a) State the point at which / has an absolute minimum: ( (b) State the point at which / has an absolute maximum: ( (c) Complete each of the following statements: () The function attains a local ? at = = 2 (il) The function attains a local 7 va- 4 (ii) The function attains a local ? v ac = 5. (1 point) Suppose /(z) = ze , 0

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

(1 point) Consider the function f(x) = 8+7xx2 1. f is increasing on the intervals 555 2. f is decreasing on the intervals iii 3. The relative maxima off occur at x = 555 4. The relative minima off...

Q 1. (05.03 MC) The table of values for f'(x) describes the behavior of continuous function f. Which of the following is true? (1 point) x 0 1 2 3 4 f'( x) -1 0 2 05 Of is increasing on (1, 3) only...

(x + 1)3 (1 point) Consider the graph of the function f (x) = W x A. What is the y-intercept of the graph? y = 1 For the following 3 questions, enter all possible values, separated by commas. If...

Advance function just the answer 1 to 10 Question 1 (1 point) A rational function of the form f( x) = axtb cxtd has a horizontal asymptote with equation y = a Question 7 (1 point) provided c * 0....

Question (1 Point) Consider the function / (2) = - for z # 0 and /(0) = 0 then a) f(x) is differentiable everywhere. b) f (x) is only differentiable at the origin. c) f (x) is differentiable nowhere....

1 point Consider the graph of the function f x shown below Click on the graph for a larger version A Estimate the integral f f x dx B If F is an antiderivative of the same function f and F 0 35...

need answers Homework 06B: Problem 5 Previous Problem Problem List Next Problem (1 point) Consider the function f(x) = -2x3 + 21x2 - 36x + 5. (a) Find all critical numbers coff. c = (b) f is...

(1 point) Consider the function f(x) = x3 - 5x2 + 9r - 1. (a) f is concave up for r E (b) f is concave down for T E (c) The inflection points of f occur at r =(1 point) Consider the function f(x) =...

Need Help With These Thank You (1 point) Consider the function f() = 9x + 6x- For this function there are four important intervals: (-oo, A], [A, B), (B, C'), and [C, oo) where A, and C' are the...

Please solve and show all steps B. f(x) is concave up on the region to and 1. (1 point) Consider the function f(x) = 6x + 8x-1. to For this function there are four important intervals: (-0o, A], C....

Briey describe or dene the following three items: revenues, gross profit, and net income.

In a Nash- Cournot equilibrium, does an oligopolistic firm produce at less than full capacity, at full capacity, or more than full capacity? Explain.

The income statement reports: a . the revenues, gains, expenses, and losses that have occurred during the reporting period. b . the revenues, gains, expenses, and losses at a point in time. c ....

How the coca cola company ensures low level of turnover in identified markets and at the same time maintain set level of growth and profitability

13. Think about a relationship conflict you have had in your workplace or home situation. Try to interpret the conflict from the following logical levels: a. Purpose b. Role c. Values d. Competence...

7. Imagine a communication situation in a work context or in the home situation that has made a big impression on you, positively or negatively. a. Examine now i. your own intentions ii. what you...

Personal role: This consists of service to family and friends.