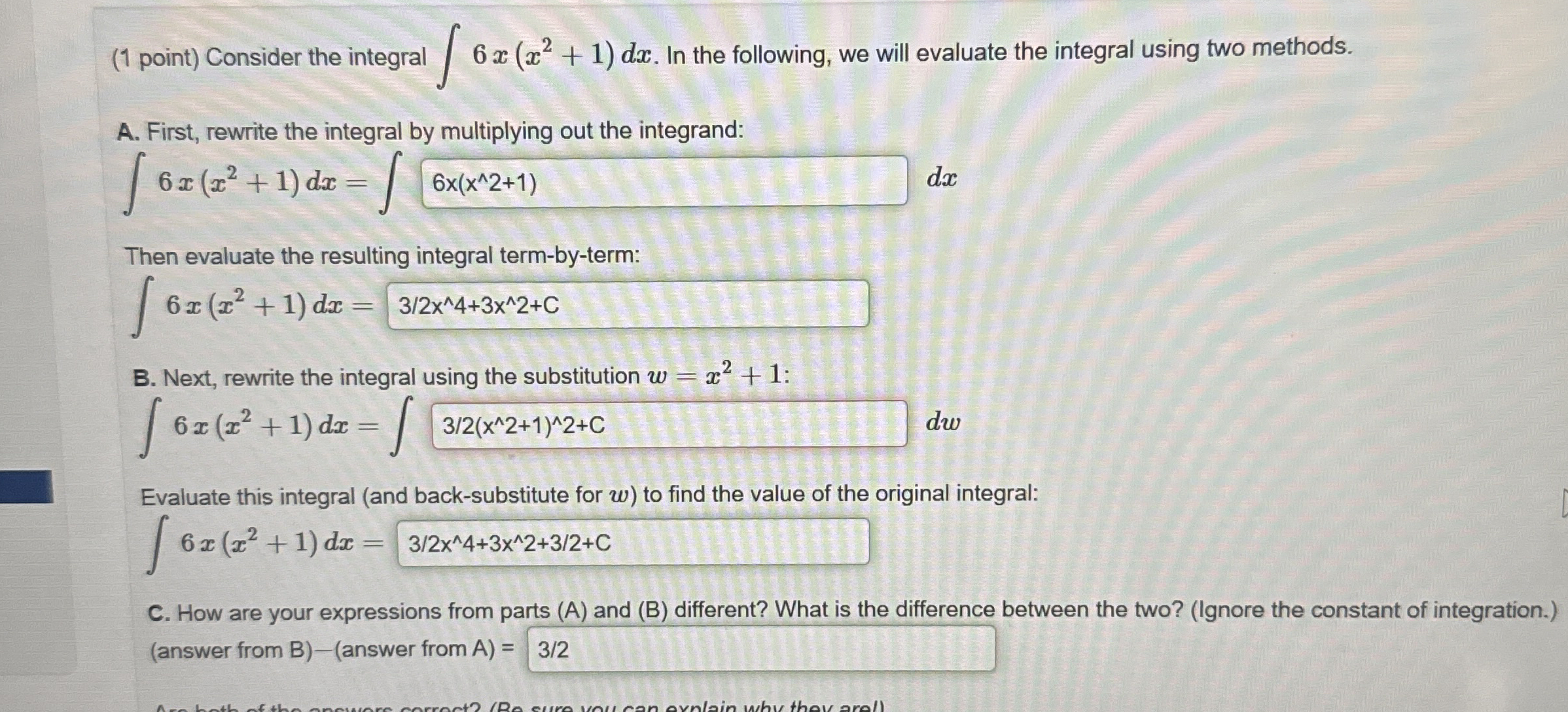
$(1$ point$)$ Consider the integral ${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}6x(x^2+1)dx.$ In the following, we will evaluate the integral using two methods.

A$.$ First, rewrite the integral by multiplying out the integrand:

${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}6x(x^2+1)dx={\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}$

Then evaluate the resulting integral term$-$by$-$term:

${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}6x(x^2+1)dx=$

$$

B$.$ Next, rewrite the integral using the substitution $w=x^2+1$ :

${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}6x(x^2+1)dx={\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}dw$

Evaluate this integral $($and back$-$substitute for $w)$ to find the value of the original integral:

${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}6x(x^2+1)dx=$

$$

C$.$ How are your expressions from parts $(A)$ and $(B)$ different? What is the difference between the two? $($Ignore the constant of integration.$)$ answer from $B$ answer from $A$