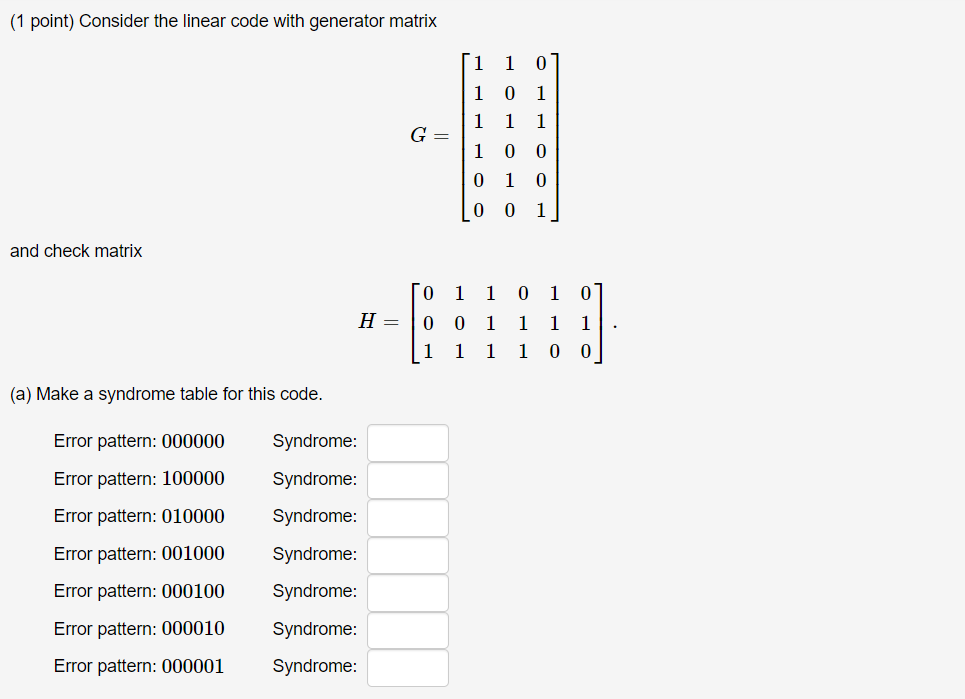
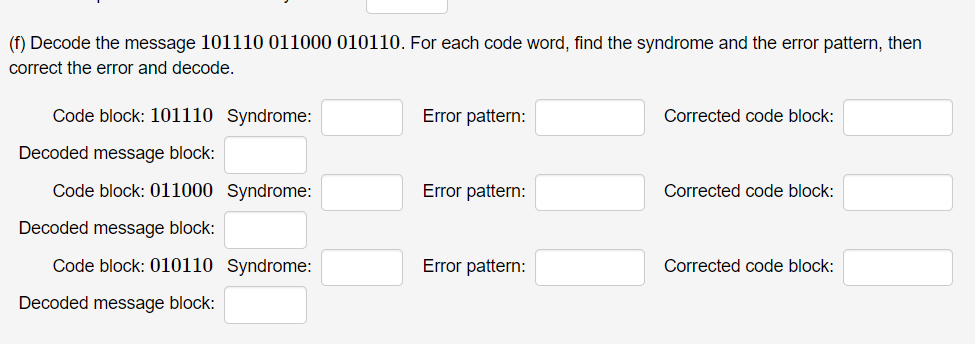
(1 point) Consider the linear code with generator matrix 1 1 0 G= 1 0 1 1 1 1 1 0 0 0 1 0 0 0 1 and check matrix 0 1 1 0 1 0 H= 0 0 1 1 1 1 . 1 1 1 0 0 (a) Make a syndrome table for this code. Error pattern: 000000 Syndrome: Error pattern: 100000 Syndrome: Syndrome: Error pattern: 010000 Error pattern: 001000 Syndrome: Error pattern: 000100 Syndrome: Error pattern: 000010 Syndrome: Syndrome: Error pattern: 000001 (f) Decode the message 101110 011000 010110. For each code word, find the syndrome and the error pattern, then correct the error and decode. Code block: 101110 Syndrome: Error pattern: Corrected code block: Decoded message block: Code block: 011000 Syndrome: Error pattern: Corrected code block: Decoded message block: Code block: 010110 Syndrome: Error pattern: Corrected code block: Decoded message block: (1 point) Consider the linear code with generator matrix 1 1 0 G= 1 0 1 1 1 1 1 0 0 0 1 0 0 0 1 and check matrix 0 1 1 0 1 0 H= 0 0 1 1 1 1 . 1 1 1 0 0 (a) Make a syndrome table for this code. Error pattern: 000000 Syndrome: Error pattern: 100000 Syndrome: Syndrome: Error pattern: 010000 Error pattern: 001000 Syndrome: Error pattern: 000100 Syndrome: Error pattern: 000010 Syndrome: Syndrome: Error pattern: 000001 (f) Decode the message 101110 011000 010110. For each code word, find the syndrome and the error pattern, then correct the error and decode. Code block: 101110 Syndrome: Error pattern: Corrected code block: Decoded message block: Code block: 011000 Syndrome: Error pattern: Corrected code block: Decoded message block: Code block: 010110 Syndrome: Error pattern: Corrected code block: Decoded message block