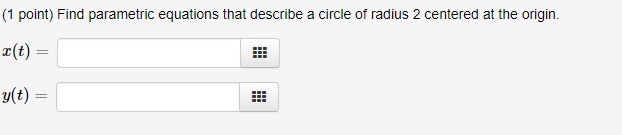
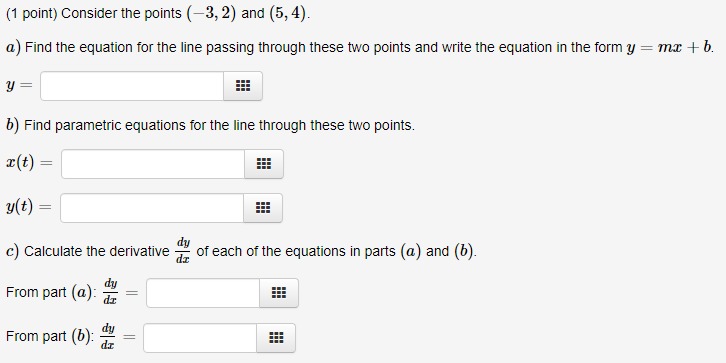
(1 point) Consider the parametric equations x = 4 + cos(t), y = 3 + sin(t). The curve traced out by these equations is a circle with radius and center ((1 point) Find parametric equations that describe a circle of radius 2 centered at the origin. x(t) = y( t ) =(1 point) The London Eye is a large Ferris wheel that has diameter 118 meters and revolves continuously. Passengers enter the cabins at the bottom of the wheel and complete one revoluljon in about 32 minutes, One minute into the ride a passenger is rising at 0,038 mils, How fast is the horizontal motion of the passenger at that moment? Hints: Write an equation for the height, in meters, of a passenger at time t, in minutes' and remember that an equation for a circle of radius 1" centered at (a,b) is (z (I)? + (y 1'02 : r2, Horizontal Speed: W8 {1 point]: Consider the points (3, 2} and (5,4). a} Find the equation for the line passing through these two points and write the equation in the form 1.! = me: + b. y = as it} Find parametno equations for the line through these two points. z} = es mi} = _ 555 e} Calculate the derivative g of each of the equations in parts {a} and (b). in ... From part [a]: E From part (b): E