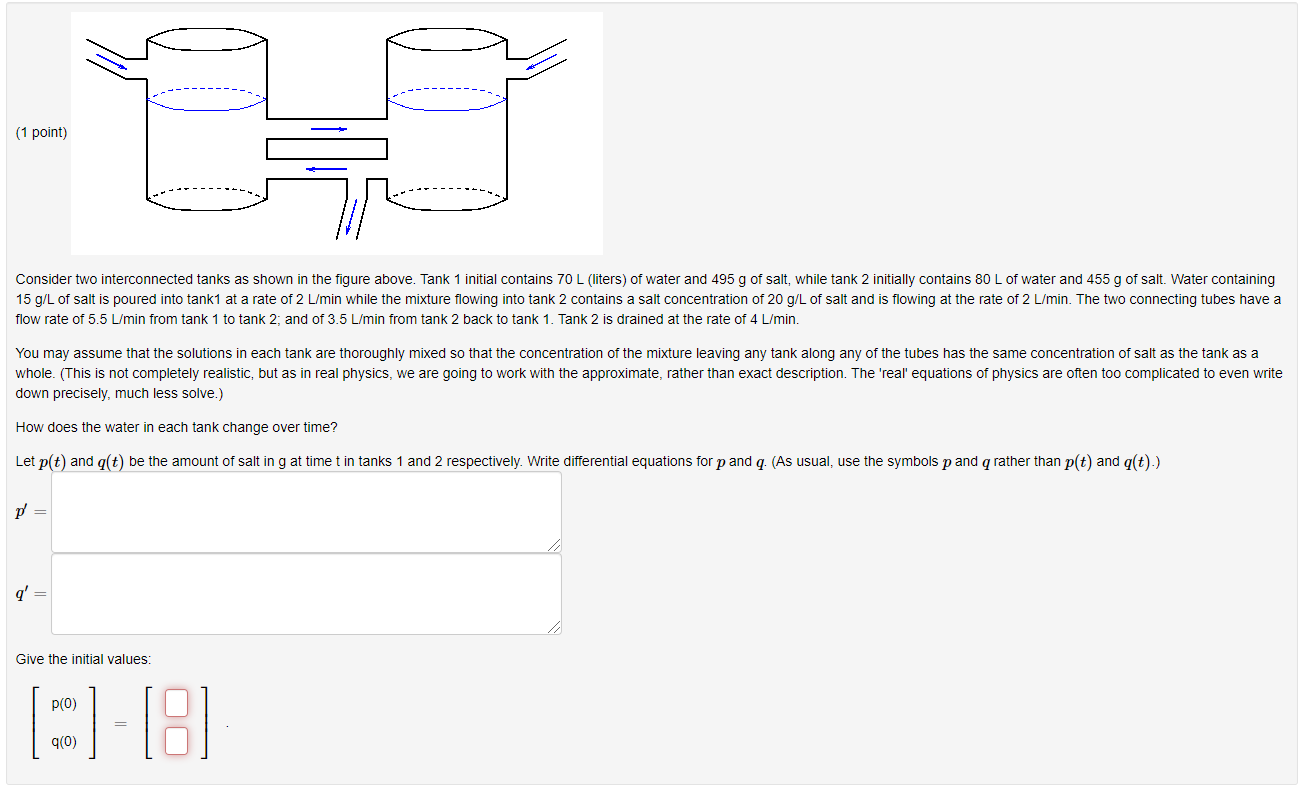
(1 point) Consider two interconnected tanks as shown in the figure above. Tank 1 initial contains 70 L (liters) of water and 495 g of salt, while tank 2 initially contains 80 L of water and 455 g of salt. Water containing 15 g/L of salt is poured into tank1 at a rate of 2 L/min while the mixture flowing into tank 2 contains a salt concentration of 20 g/L of salt and is flowing at the rate of 2 L/min. The two connecting tubes have a flow rate of 5.5 L/min from tank 1 to tank 2; and of 3.5 L/min from tank 2 back to tank 1. Tank 2 is drained at the rate of 4 L/min. You may assume that the solutions in each tank are thoroughly mixed so that the concentration of the mixture leaving any tank along any of the tubes has the same concentration of salt as the tank as a whole. (This is not completely realistic, but as in real physics, we are going to work with the approximate, rather than exact description. The 'real' equations of physics are often too complicated to even write down precisely, much less solve.) How does the water in each tank change over time? Let p(t) and q(t) be the amount of salt ing at time t in tanks 1 and 2 respectively. Write differential equations for p and q. (As usual, use the symbols p and q rather than p(t) and q(t).) P' g' Give the initial values: 1 8% ] - 18]