Question: (1 point) cos Suppose that f (# ) = -8 and f' () = 7, and let g(x) = f(x) sin x and h(x) =

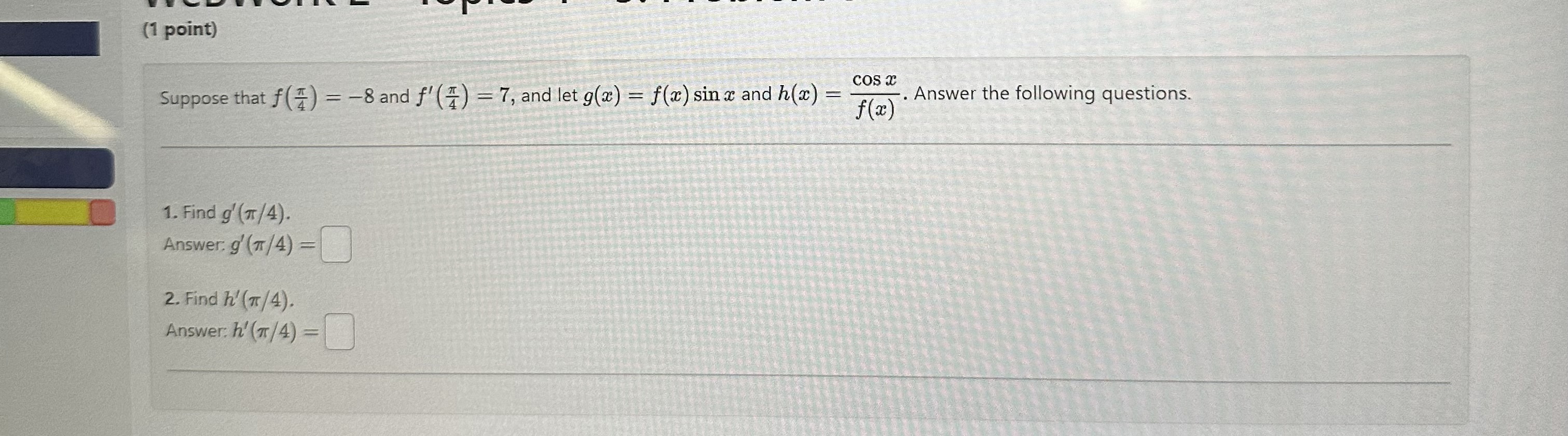
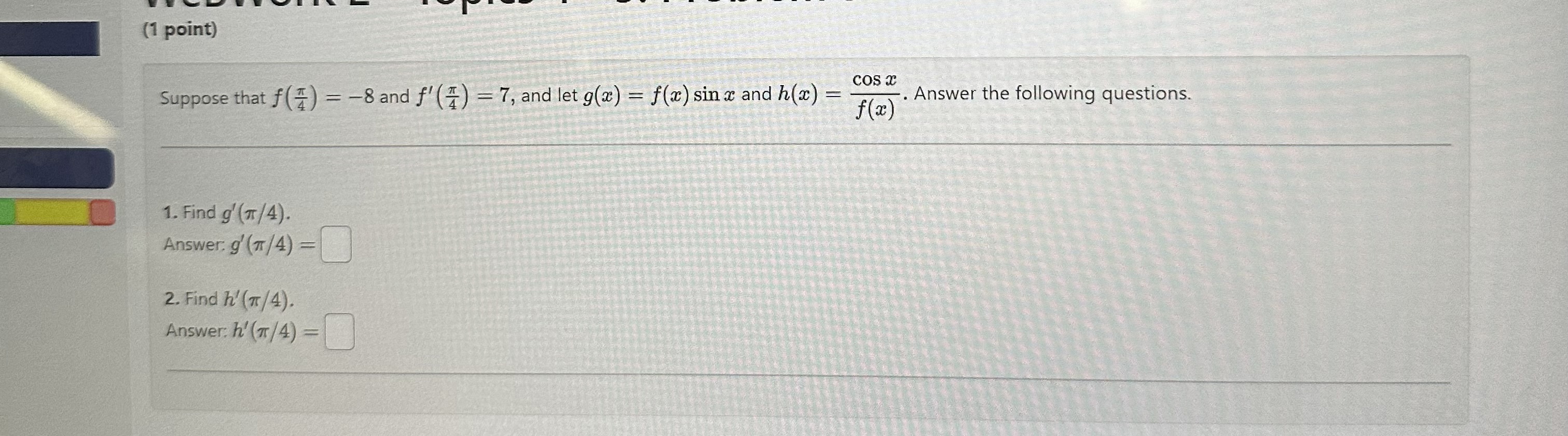
(1 point) cos Suppose that f (# ) = -8 and f' () = 7, and let g(x) = f(x) sin x and h(x) = f (z) Answer the following questions. 1. Find g' (7 / 4). Answer. g' (7 /4) = 2. Find h' (7 / 4). Answer: h'(7 / 4) =WeBWork 2 - Topics 4 - 5: Problem 14 (1 point) Suppose f is a one-to-one, differentiable function and its inverse function f is also differentiable. One can show, using implicit differentiation (do it!), that 1 ( f - 1 )' ( 20 ) = Fi (f - 1 ( 20 ) ) Find (f-1)'(-4) if f(-5) = -4 and f'(-5) = 2/11. ( f- 1 )' ( - 4 ) =1]

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

What percentage of the population live in their state of birth? According to the U.S. Census Bureau's American Community Survey, the figure ranges from 25% in Nevada to 78.7% in Louisiana. The...

Question 1 If g(a) = 2 In(a + 1) and f is a differentiable function of a, which of the following is equivalent to the derivative of f (g(a) ) with respect to a ? f' 241 2f' (x) +1 f' (2 In(x + 1))...

Please help in answering the following questions. Activity 1: Match the items column 1 with the correct value of the limit in column 2. Write the letter of the answer on the space provided before the...

1 As shown in the figure below, a camera is mounted on a point 30 m from the base of a rocket launching pad. The rocket rises vertically when launched, and the camera's angle is continually adjusted...

7. Let g (x) = CSCx f (x ) If f (- ) = 3 and f' (-") = -7, find g' (-=). (6pts) 8. Let g (x) = sec2 x f(x). Iff () = 4 and f' ( ) = 5, find g' . (6pts) 9 . Find all x values where f (x) = = tan x +...

Hi, step by step solutions please! Consider the function f (x) = g(x)h(x). The values of the functions g, h and their first and second derivatives at the point x = 4 are given by the following table:...

10. At time t (in days), the size S of a population of butterflies is given by the formula 600 S = 1+49(0.6)' Use the graph below and your knowledge of derivatives to answer the following: (6 marks)...

........... (1 point) Let g(x) = j: f (t) (it, where f is the function whose graph is shown. Answer the following questions only on the interval [0, 10]. 1. At what values of x does g have a local...

Rodriguez managed a Walmart store at Fajardo, Puerto Rico. Following an evaluation, his performance was considered unsatisfactory, and he was demoted to assistant manager at another store. Rodriguez...

Construct a method which can calculate square value of number Hints: Using the ** operator

Which firm seems the best prepared for internationalization? a firm that sellis its products orify to those forelpe customers who directly condact the firm firm that has a pardurtion capacity that is...

It Bikess management wants to make sure it has policies and procedures in place to protect the privacy of visitors to its Web site. You have been asked to develop Dirt Bikess Web site privacy policy....

Q1. Outline two moral justifications for capitalism. What do you see as the key strengths and weaknesses of each justification? Q2. Do you think that the criticisms of capitalism are warranted? Q3....

Tori and some other childeen experimented with balls to see which ones rolled. First using a piece of cardboard to use as a ramp, they angled it on a block to the floor to test the balls. Then Tori...

Identify two potential substitutes for corporate diversification.

Define the concept of economies of scope and identify eight potential economies of scope a diversified firm might try to exploit.

In each of the pairs given below, which firm is more vertically integrated? Visit the company Web sites to gather supporting information. (a) Vodafone and Airtel (b) Adolph Coors Brewing and Heineken...