Question: (1 point) Define L : P3 - P3 by L(p(x)) = p(0)x2 + p' (0). It is easy to verify that L is a linear

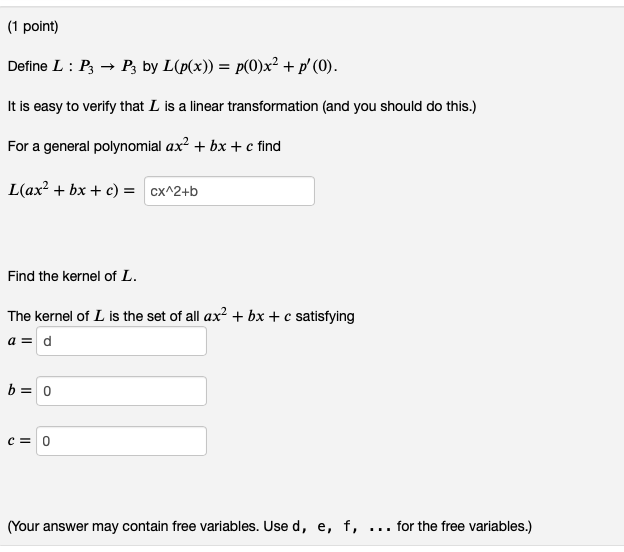
(1 point) Define L : P3 - P3 by L(p(x)) = p(0)x2 + p' (0). It is easy to verify that L is a linear transformation (and you should do this.) For a general polynomial ax + bx + c find L(ax' + bx + c) = cx^2+b Find the kernel of L. The kernel of L is the set of all ax~ + bx + c satisfying 0= d b = 0 CE 0 (Your answer may contain free variables. Used, e, f, . . . for the free variables.)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Fraction of hosts infected Case Study 2 Hosts, Parasites, and Time-Travel 0.8 0.6 0.4 0.2 0 Past Contemporary Future Time Figure \u00031 Horizontal axis is the time from which the parasite was taken,...

solve the answers handwritten but please type all the final answers together in the different section after solving. Thanks. 1. [-11 Points] DETAILS SCALCETQ 14.6.004.EP. Consider the following. x,...

P3 X fi V B H 1 1 K L M N 0 P Q R S T U V W z z AB AC AC D E F G J 1 ASSIGNMENT TOPICS 2 Master Budget for a Merchandiser Knockoffs Unlimited, a nationwide distributor of low-cost imitation designer...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

8.4 Write on paper for upvote please. Questions: 12, 17, 22 8.4 Matrices for General Linear Transformations 485 b. Verify that Formula (8) holds for every vector in R'. d. Use the formula obtained in...

Convex geometry 0.1 Dehn-Sommerville relations In this section we will talk about convex polytopes. One possible denition of a convex polytope uses the notion of a half-space: A closed half-space in...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

The acquittal of John Felderhof, the former chief geologist for Bre-X Minerals, and the settlement with Andrew Rankin, the former RBC Dominion Securities managing director (see page 371), represent...

On January 14, 2016, Nokia and Alcatel-Lucent celebrated their first day of combined operations. A couple of years earlier, Nokia and Microsoft formed a partnership, which did not work well. Why did...

identify data that would be useful for a management accounting dashboard

A company is preparing completing their Cash Budget. The following data has been prepared for cash receipts and payments. January February March Cash receipts $1,061,200 $1,182,400 $1,091,700 Cash...