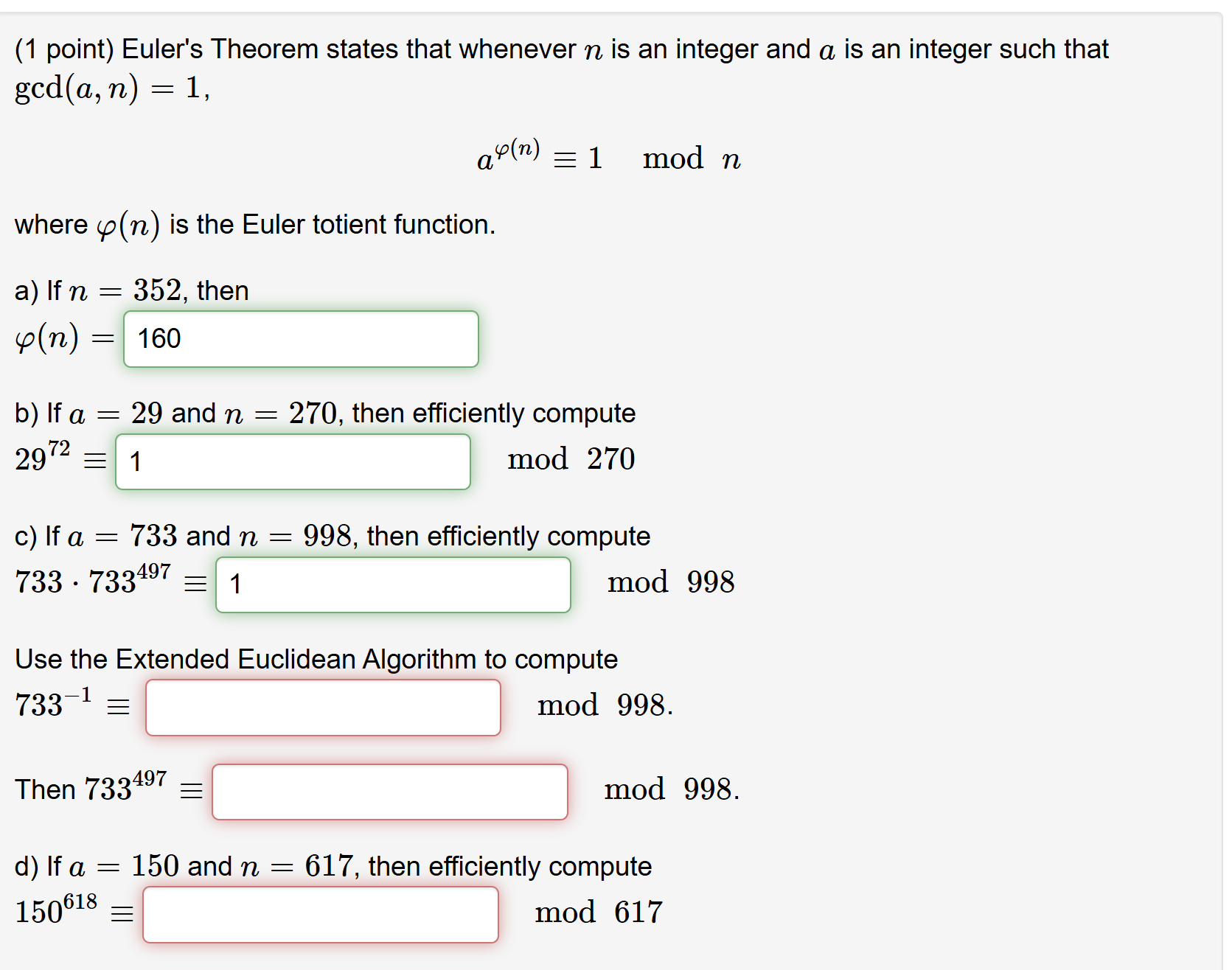
$(1$ point$)$ Euler's Theorem states that whenever $n$ is an integer and $a$ is an integer such that

$gcd(a,n)=1$

$a^{(n)}-=1,$modn

where $(n)$ is the Euler totient function.

a$)$ If $n=352,$ then

$(n)=$

b$)$ If $a=29$ and $n=270,$ then efficiently compute

${29}^{72}-=$

mod$270$

c$)$ If $a=733$ and $n=998,$ then efficiently compute

$733*{733}^{497}-=$

mod$998$

Use the Extended Euclidean Algorithm to compute

${733}^{-1}-=$

mod$998.$

Then ${733}^{497}-=$

mod$998$

d$)$ If $a=150$ and $n=617,$ then efficiently compute

${150}^{618}-=$

mod$617$