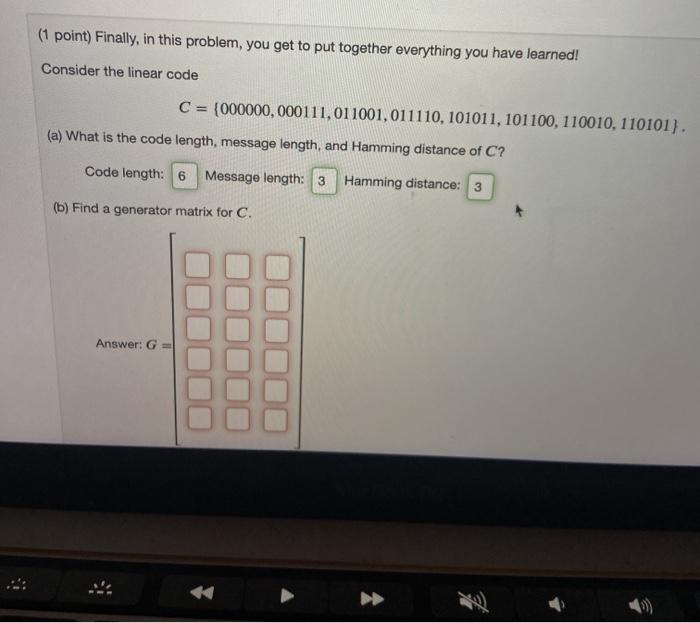
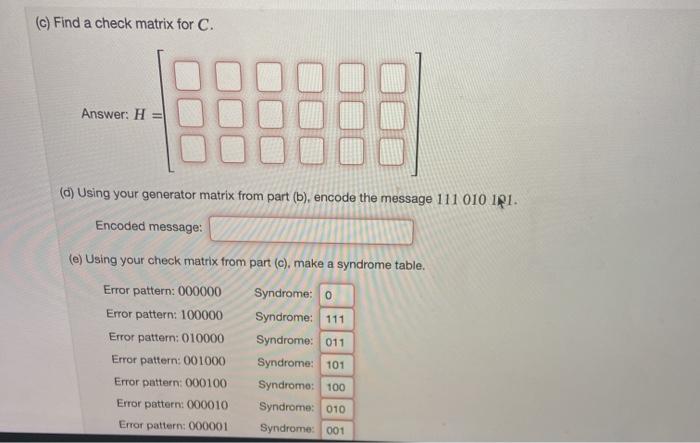
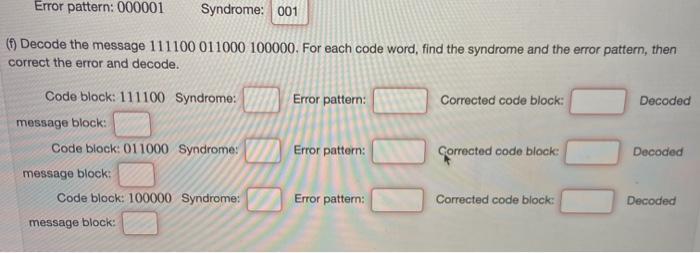
(1 point) Finally, in this problem, you get to put together everything you have learned! Consider the linear code C = {000000, 000111, 011001,011110, 101011, 101100, 110010, 110101). (a) What is the code length, message length, and Hamming distance of C? Code length: 6 Message length: 3 Hamming distance: 3 (b) Find a generator matrix for C. Answer: G (c) Find a check matrix for C. Answer: H = (d) Using your generator matrix from part (b), encode the message 111 010 IPI. Encoded message: (e) Using your check matrix from part (c), make a syndrome table. Error pattern: 000000 Error pattern: 100000 Error pattern: 010000 Error pattern: 001000 Error pattern: 000100 Syndrome: 0 Syndrome: 111 Syndrome: 011 Syndrome: 101 Syndrome: 100 Syndrome: 010 Syndrome: 001 Error pattern: 000010 Error pattern: 000001 Error pattern: 000001 Syndrome: 001 Decode the message 111100 011000 100000. For each code word, find the syndrome and the error pattern, then correct the error and decode. Code block: 111100 Syndrome: Error pattern: Corrected code block: Decoded message block: Code block: 011000 Syndrome: Error pattern: Corrected code block Decoded message block: Code block: 100000 Syndrome: Error pattern: Corrected code block: Decoded message block