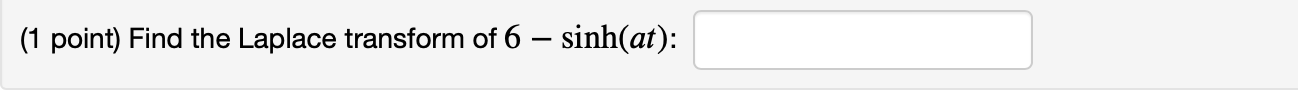
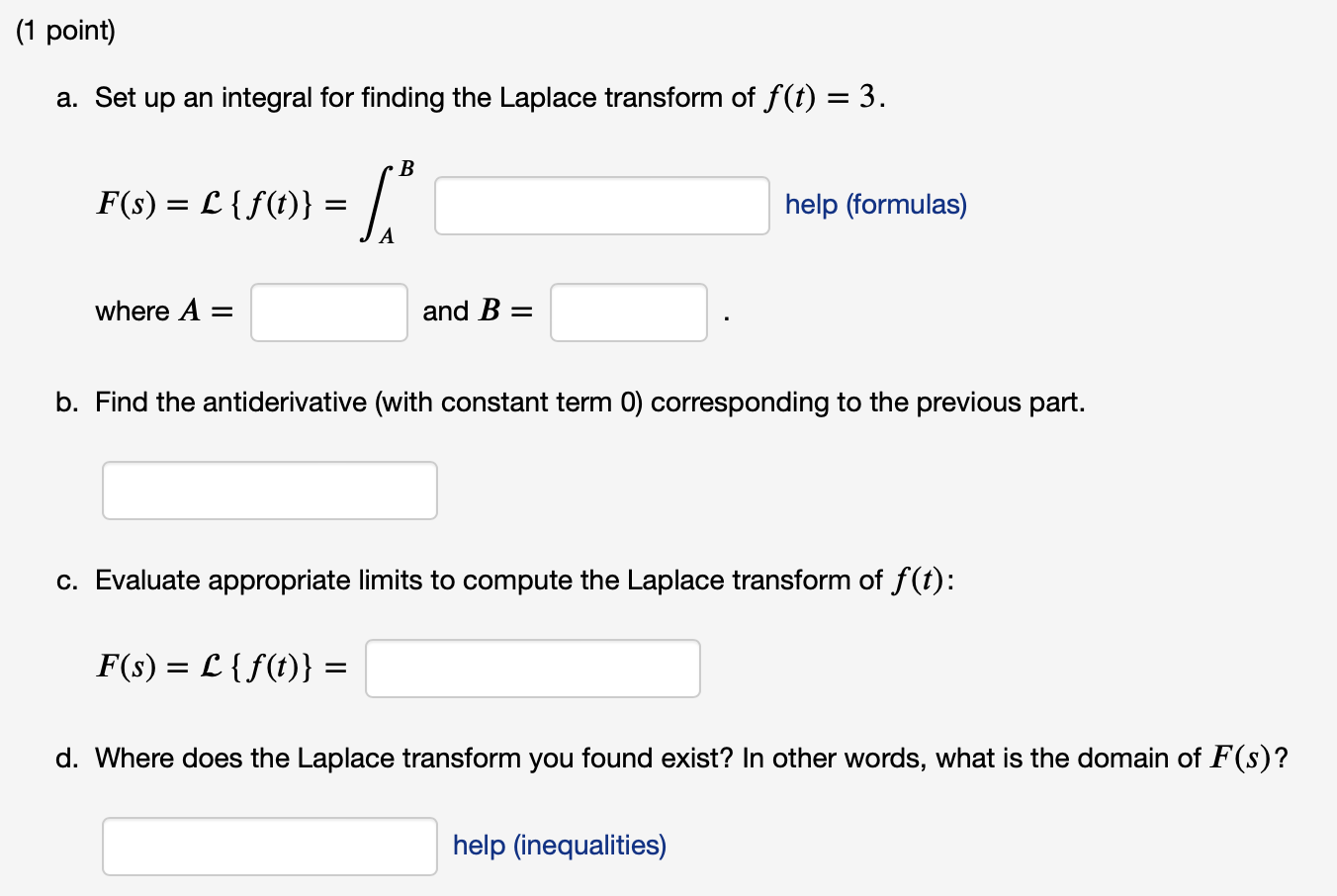
(1 point) Find the Laplace transform F(s) = [ {f(t) } of the function f(t) = (3 - t)(h(t - 5) - h(t - 8)), for s * 0. F(s) = [{ f(t) } = help (formulas)\f(1 point) a. Set up an integral for finding the Laplace transform of f (I) = 3. B F(S) = E {1%)} = / help (formulas) A where A = and B = b. Find the antiderivative (with constant term 0) corresponding to the previous part. c. Evaluate appropriate limits to compute the Laplace transform of f (1'): HS) = E {f(r)} = d. Where does the Laplace transform you found exist? In other words, what is the domain of F (5)? help (inequalities)