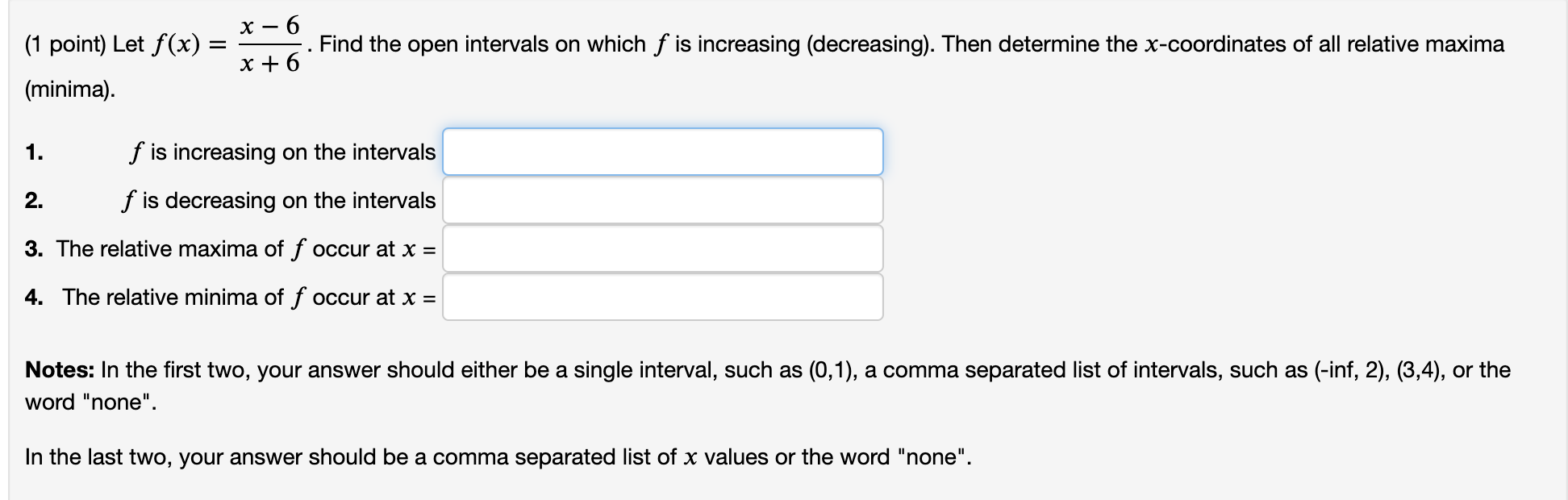
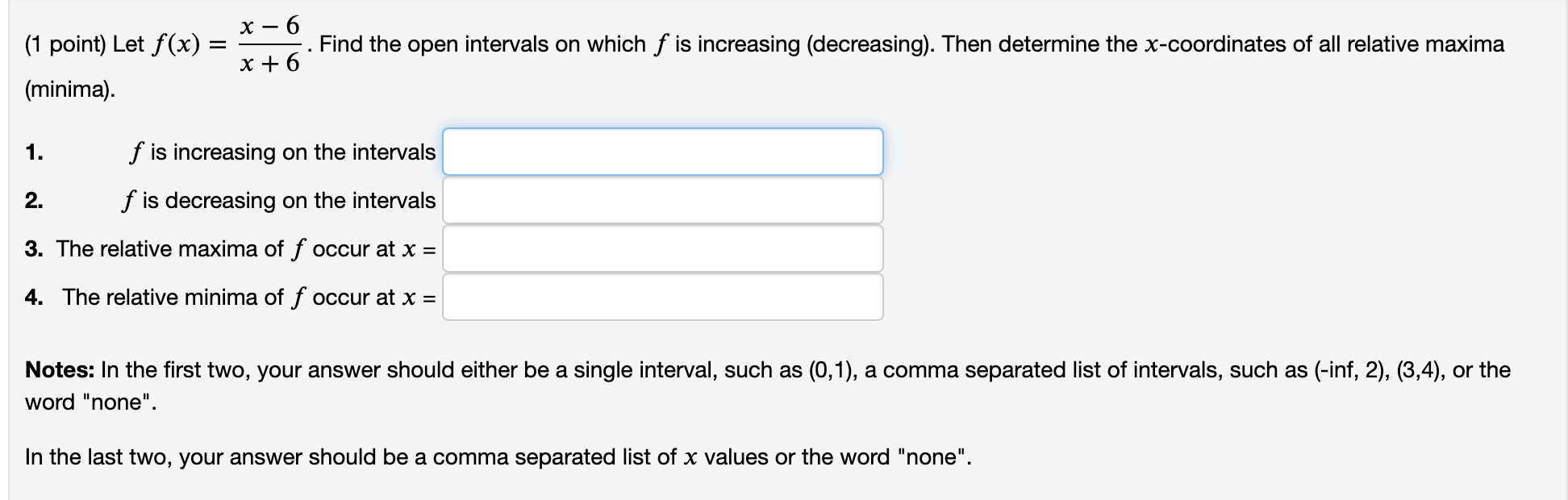
(1 point) For x E [11, 12] the function f is defined by f(x) = x7(x + 4)2 On which two intervals is the function increasing (enter intervals in ascending order)? to and to Find the region in which the function is positive: to Where does the function achieve its minimum? x6 (1 point) Let f (x) = . Find the open intervals on which f is increasing (decreasing). Then determine the x-coordinates of all relative maxima x + 6 (minima). 1. f is increasing on the intervals 2. f is decreasing on the intervals 3. The relative maxima of f occur at x = 4. The relative minima of f occur at x = Notes: In the first two, your answer should either be a single interval, such as (0,1), a comma separated list of intervals, such as (-inf, 2), (3,4), or the word "none". In the last two, your answer should be a comma separated list of x values or the word "none"