Question: (1 point) How many pivot variables does each augmented matrix have? 1 -2 -5 a. Choose 0 0 0 0 0 0 1 b.

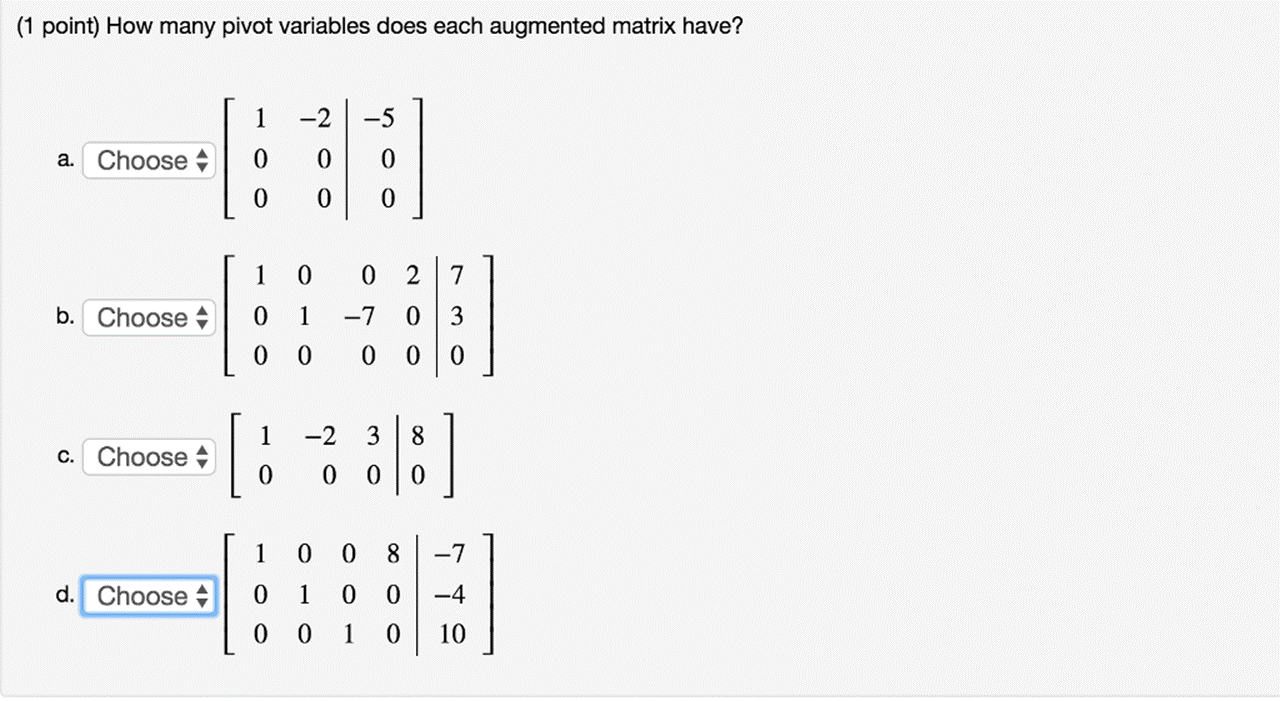
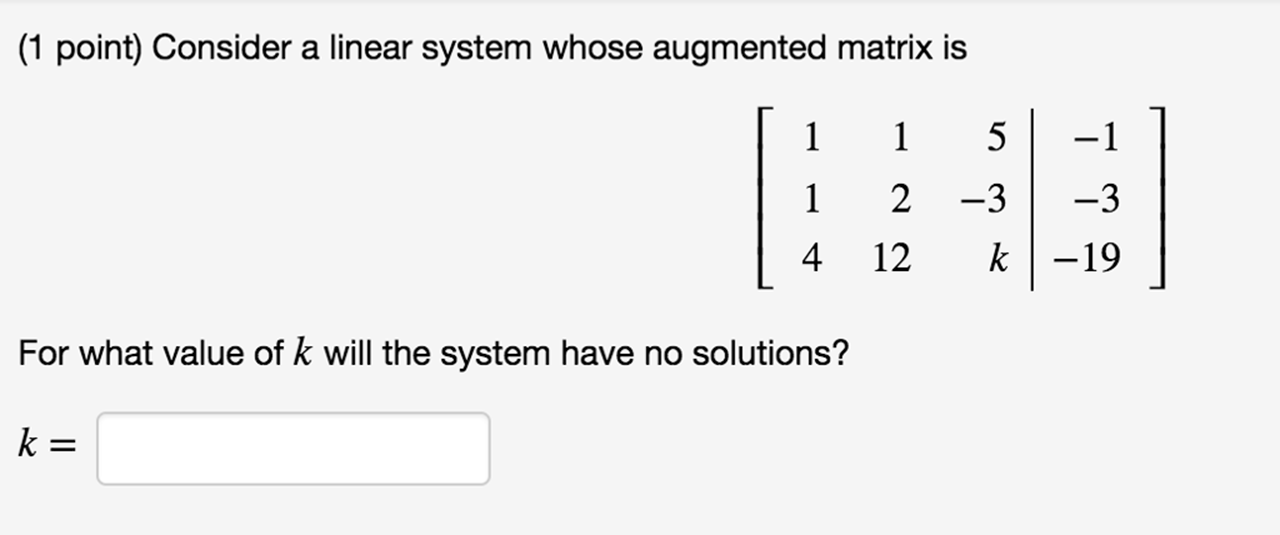
(1 point) How many pivot variables does each augmented matrix have? 1

-2 -5 a. Choose 0 0 0 0 0 0 1 b.

Choose 0 0 c. Choose d. Choose 1 0 0 1 -7

(1 point) How many pivot variables does each augmented matrix have? 1 -2 -5 a. Choose 0 0 0 0 0 0 1 b. Choose 0 0 c. Choose d. Choose 1 0 0 1 -7 0 0 0 0 -2 3 0 0 0 0 8 -7 00 -4 0 1 0 10 0 2 7 3 0 1 0 1 0 80 6x - 3y - 3z = -30 -x - 2y + 4z x - 5y + 2z = 35 = 30 How many solutions are there to this system? A. None B. Exactly 1 C. Exactly 2 D. Exactly 3 E. Infinitely many F. None of the above If there is one solution, give its coordinates in the answer spaces below. If there are infinitely many solutions, enter the parameter t in the answer blank for z., enter a formula for y in terms of t in the answer blank for y and enter a formula for x in terms of t in the answer blank for x. If there are no solutions, leave the answer blanks for x, y and z empty. X = y = 7. = (1 point) Consider a linear system whose augmented matrix is 1 1 5 1 2 -3 4 12 k For what value of k will the system have no solutions? k= -1 -3 -19

Step by Step Solution

★★★★★

3.44 Rating (151 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To solve this system of equations we can rewrite them in matrix form ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

How many pivot columns must a 4 ( 6 matrix have if its columns span? Why? R4

How many pivot columns must a 6 ( 4 matrix have if its columns are linearly independent? Why?

Pivot each matrix about the circled element. 1. 2. (3 -6 4 6. -5 11 (2) -3 6.

1.) [DA2] Multiple Choice. Answer: Analysis of variance is a statistical method of comparing the of several populations. a. Standard deviations b. Variances c Means d. Proportions e None of the above...

II. Problems - You have to show your work. No credit without an explanation (20 marks each). 1. Consider the following graph of TMSE vs. GMSE on the vertical axis and the number of independent...

Game theory Two players play the following stage-game twice in a row (T = 2), and observe each other's first-stage action before choosing actions in the second stage. Both players discount...

How many main feasts does each Eastern Pueblo have today? Group of answer choices 1 4 2 3 When do those feasts occur? Group of answer choices Spring and Fall Summer, Winter, Spring, and Fall Summer an

QUESTION 1 Consider a Markov chain with (one-step) transition probability matrix P= How many communicating classes does the Markov chain have? QUESTION 2 Consider a Markov chain with (one-step)...

A closed container initially holds 50 monatomic A particles that have a combined energy of 120 units. After 100 monatomic $B$ particles with a combined energy of 180 units are added to the...

Asset turnover ratio Financial statement data for years ended December 31, 2023 and 20Y2, for Edison Company follow: 2013 20Y2 Sales $1,694,000 $1,438,500 Total assets: Beginning of 730,000 640,000...

Income Statement for the ear Ended 3 0 Net Saies ( All on Credit ) . 7 4 1 8 COGS. 5 2 7 1 Depreciation. 7 4 5 EBIT 1 4 0 2 Interest. 3 0 5 . Taxes 3 8 4 Net Incorne. 7 1 3 Dividends paid 2 5 0...

When prioritizing risk, what are the two primary criteria that need to be determined for analyzing the level of risk for a particular event? Using these two criteria, how would you describe the risk...

Tanya ( born 1 0 - 3 1 - 9 0 ) is single, has no dependents and will not itemize deductions. She cannot be claimed as a dependent by anyone else. Tanya can claim adjustments of $ 8 0 0 for her...

Bugs NoMore Company manufactures a product effective in controlling beetles. The company uses a standard cost system and a flexible budget. Standard cost of a gallon is as follows: Direct material: 2...

Your director at the department of Home Affairs has appointed you as the lead project manager for a project to rollout the new card type identification to all South African citizens, replacing the...

A new project would require an immediate increase in raw materials in the amount of $ 3 , 0 0 0 . The firm expects that accounts payable will automatically increase $ 1 5 0 0 . How much must the firm...

Which of the companies has the lowest accounts receivable turnover in the year 20X2? a. Company A. b. Company B. c. Company C. d. CompanyD. 20X1 20X2 Credit Sales Average Receivables Balance $1.0...

For what value(s) of h is b in the plane spanned by a1 and a2? Let 3 -5 and b -8 3 az

Determine the area of the parallelogram determine by the points (1, 4), (-1, 5), (3, 9), and (5, 8). How can you tell that the quadrilateral determined by the points is actually a parallelogram?

Solve the systems in exercises 1-2. 1. x2 + 5x3 = -4 x1 + 4x2 + 3x3 = -2 2x1 + 7x2 + x3 = -2 2. x1 - 5x2 + 4x3 = -3 2x1 - 7x2 + 3x3 = -2 -2x1 + x2 + 7x3 = -1

Determine the following values associated with a Poisson distribution with t equal to 3: a. P (x 3) b. P (x > 3) c. P (2 0.50.

A population of 10 items contains 3 that are red and 7 that are green. What is the probability that in a random sample of 3 items selected without replacement, 2 red and 1 green items are selected?

A corporation has 11 manufacturing plants. Of these, seven are domestic and four are located outside the United States. Each year, a performance evaluation is conducted for 4 randomly selected...