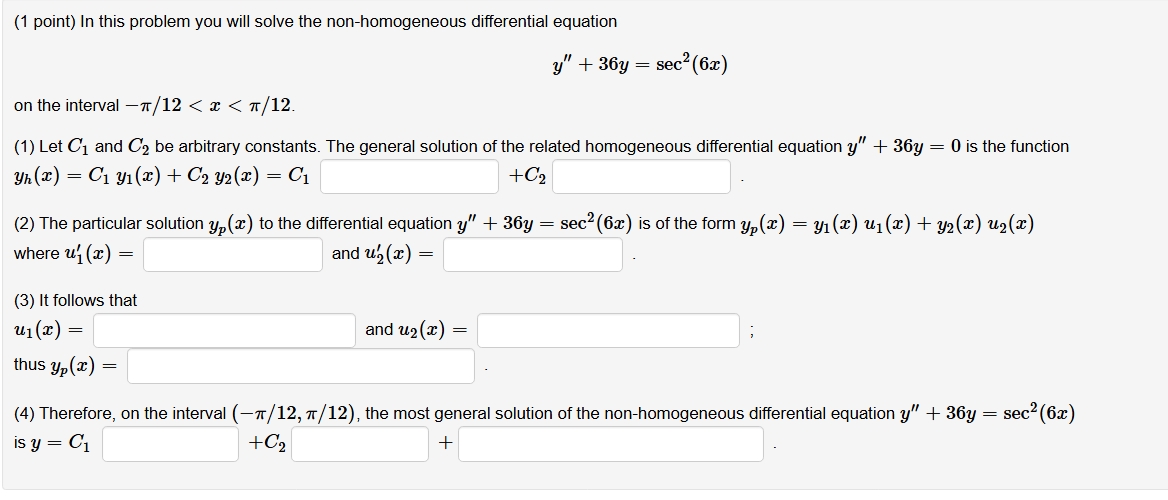
$(1$ point$)In$ this problem you will solve the non$-$homogeneous differential equation

$y^{\text{'}\text{'}}+36y=se{c}^2(6x)$

$on$ the interval $C_1{C}_2{y}^{\text{'}\text{'}}+36y=0y_h(x)=C_1{y}_1(x)+C_2{y}_2(x)=C_1+C_2{y}_p(x)y^{\text{'}\text{'}}+36y=se{c}^2(6x)y_p(x)=y_1(x)u_1(x)+y_2(x)u_2(x)u_1^{\text{'}}(x)=u_2^{\text{'}}(x)=u_1(x)=u_2(x)=y_p(x)=(-\frac{}{12},\frac{}{12})y^{\text{'}\text{'}}+36y=se{c}^2(6x)y=C_1+C_2+-\frac{}{12.}$

$(1)$ Let $C_1$ and $C_{2}be$ arbitrary constants. The general solution $of$ the related homogeneous differential equation $y^{\text{'}\text{'}}+36y=0is$ the function

$y_h(x)=C_1{y}_1(x)+C_2{y}_2(x)=C_1$

$+C_2$

$(2)$ The particular solution $y_p(x)to$ the differential equation $y^{\text{'}\text{'}}+36y=se{c}^2(6x)isof$ the form $y_p(x)=y_1(x)u_1(x)+y_2(x)u_2(x)$

where $u_1^{\text{'}}(x)=$

and $u_2^{\text{'}}(x)=$

$.$

$(3)It$ follows that

$u_1(x)=$

and $u_2(x)=$

;

thus $y_p(x)=$

$(4)$ Therefore, $on$ the interval $(-\frac{}{12},\frac{}{12}),$ the most general solution $of$ the non$-$homogeneous differential equation $y^{\text{'}\text{'}}+36y=se{c}^2(6x)$

$isy=C_1$

$+C_2$

$+$

$.$ ANSWER ALL $OF$ THE BLANKS PLEASE!!!