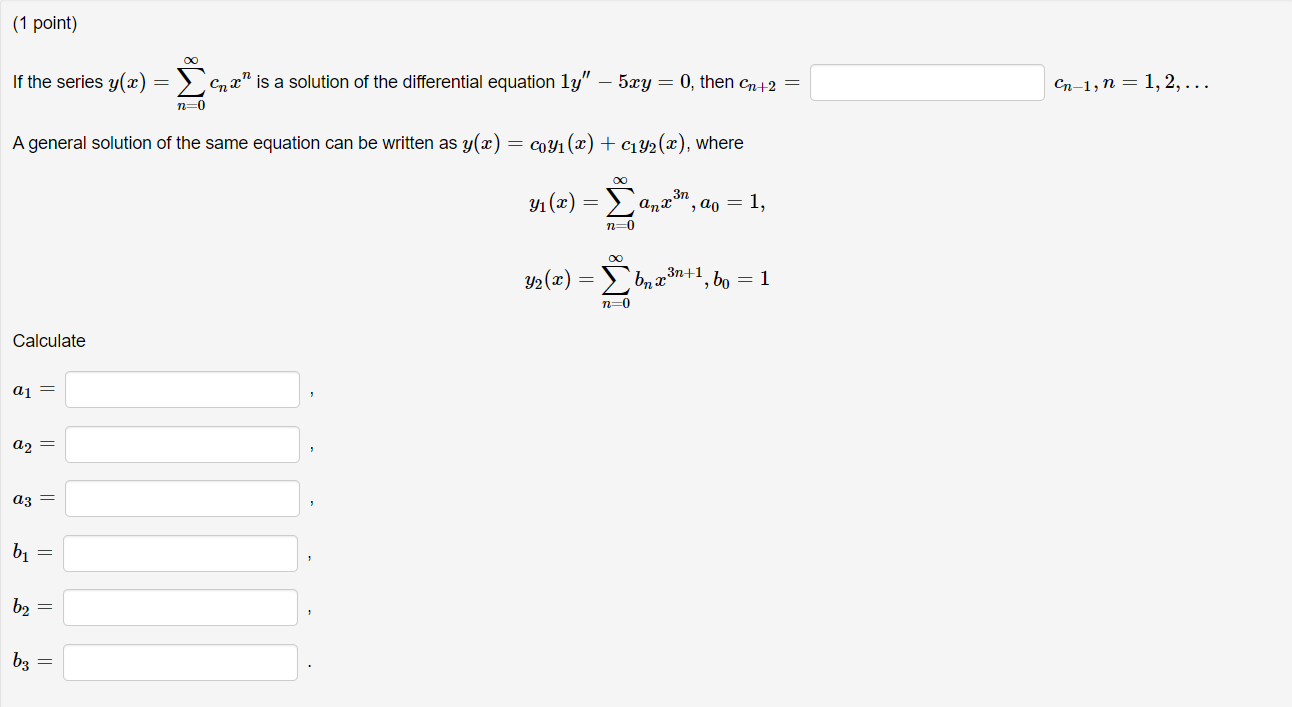
(1 point) If the series y(a) = > Cn a" is a solution of the differential equation ly" - 5xy = 0, then Cn+2 = n=0 Cn-1, n = 1, 2, ... A general solution of the same equation can be written as y(x) = coy (x) + cly/2 (), where y1 (x) => and3, do = 1, n=0 y2 (x) = bn a3+1, bo = 1 n=0 Calculate 01 = a2 = 03 = by = bo = ba =since, Here we have C3 = 5 Co 6 Cy = 5 12 CS = 5 20 CB = 5 30 C3 C7 = Cy 42 In general, Cnitz = 5 Cn - 1 (h+1) (n+2) # n = 1 , 2, 3, 4 , . .. .. this is required entry in first blank