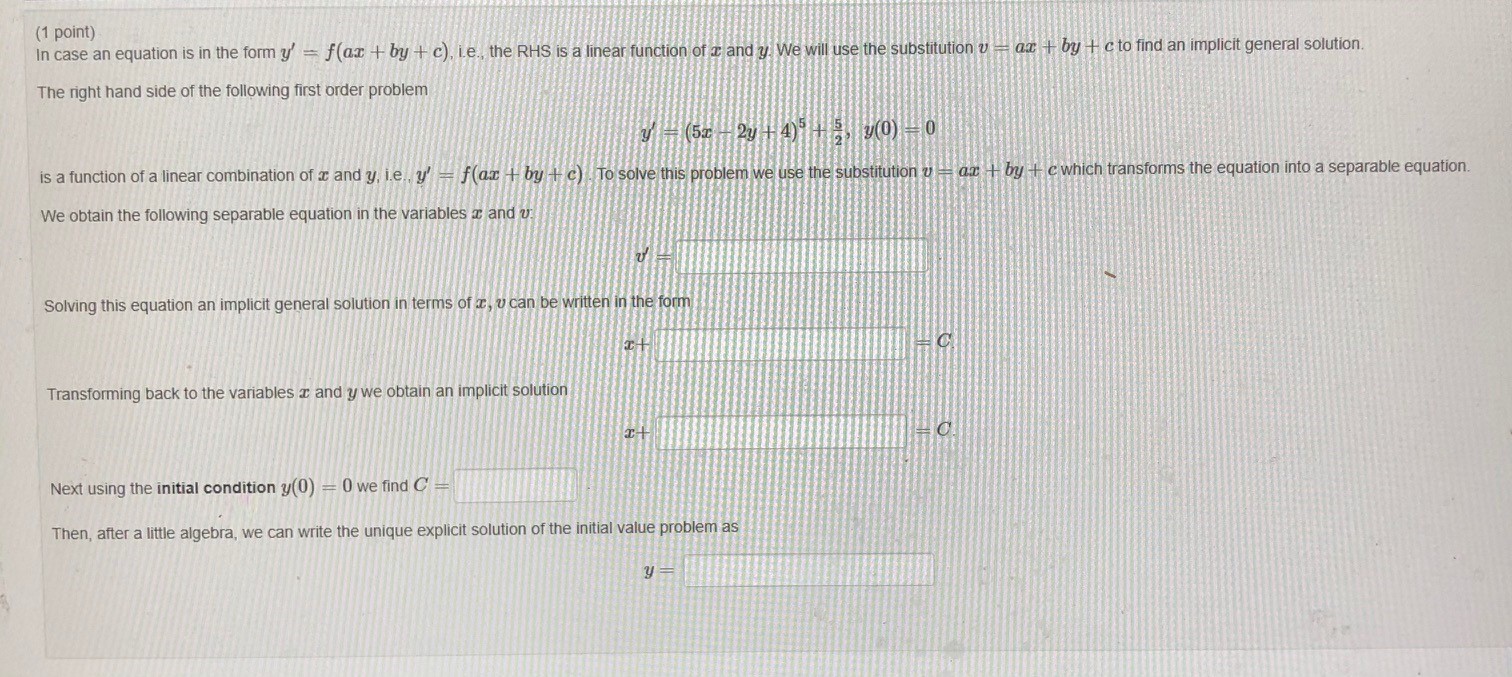
(1 point) In case an equation is in the form y' = f(ar + by + c), Le., the RHS is a linear function of I and y. We will use the substitution v - ar + by | c to find an implicit general solution. The right hand side of the following first order problem y (52 27 1 4)54 5 9(0) -0 is a function of a linear combination of c and y, i.e., y' - f(ax + by + c) . To solve this problem we use the substitution u tax + by + c which transforms the equation into a separable equation. We obtain the following separable equation in the variables c and v. Solving this equation an implicit general solution in terms of I, u can be written in the form C Transforming back to the variables a and y we obtain an implicit solution Next using the initial condition y(0) = 0 we find C Then, after a little algebra, we can write the unique explicit solution of the initial value problem as