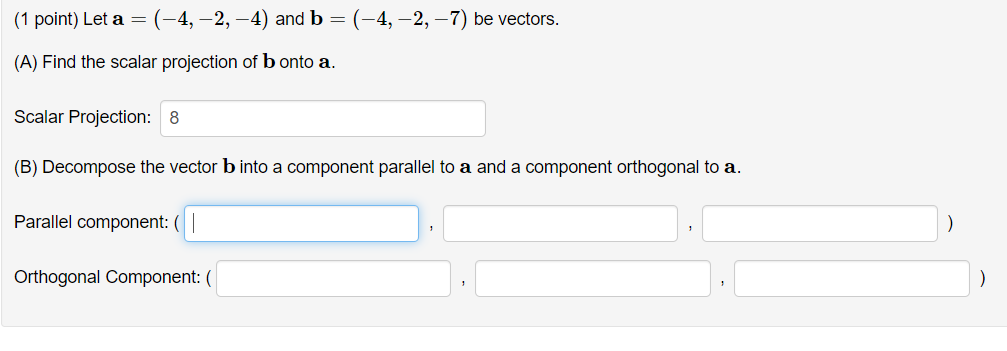
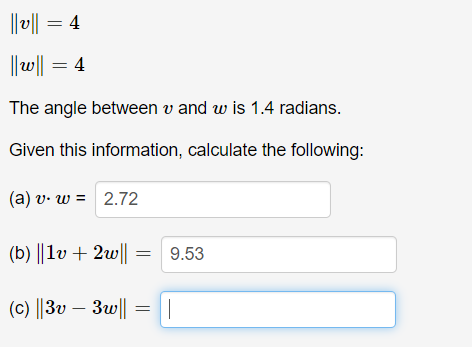
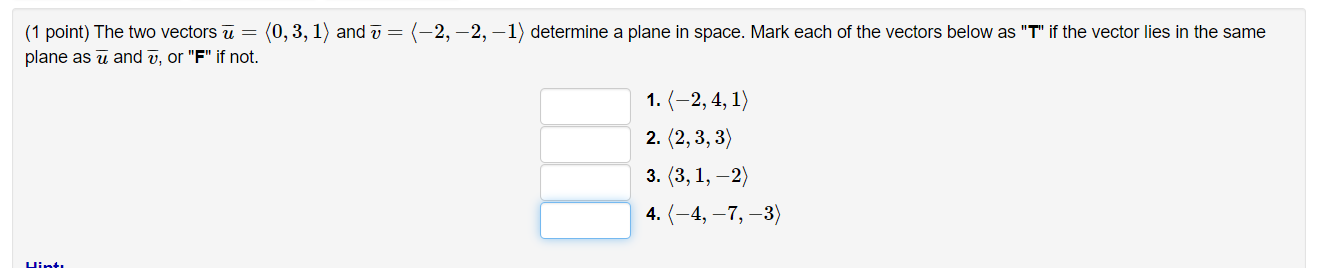
(1 point) Let a = (-4, -2, -4) and b = (-4, -2, -7) be vectors. (A) Find the scalar projection of b onto a. Scalar Projection: 8 (B) Decompose the vector b into a component parallel to a and a component orthogonal to a. Parallel component: ( Orthogonal Component: (1/ w|1 = 4 1/ 20|1 =4 The angle between v and w is 1.4 radians. Given this information, calculate the following: (a) v. w = 2.72 (b) |/1v + 2wll = 9.53 (c) 3v - 3w| =(1 point) The two vectors u = (0, 3, 1) and v = (-2, -2, -1) determine a plane in space. Mark each of the vectors below as "T" if the vector lies in the same plane as u and v, or "F" if not. 1. (-2, 4, 1) 2. (2, 3, 3) 3. (3, 1, -2) 4. (-4, -7, -3)