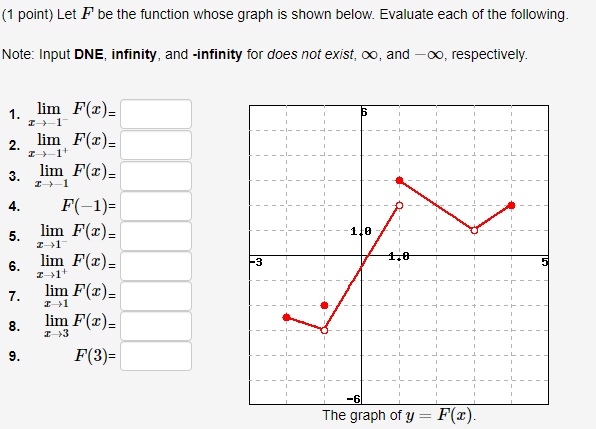
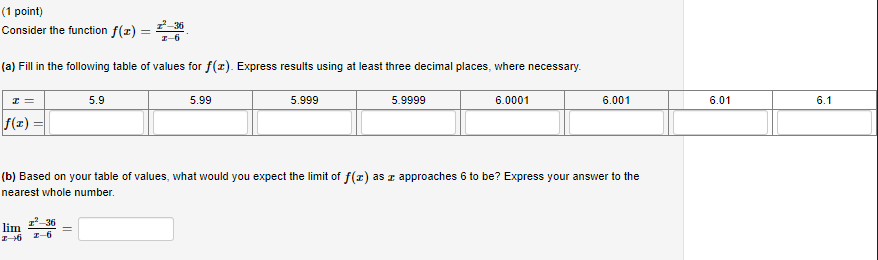
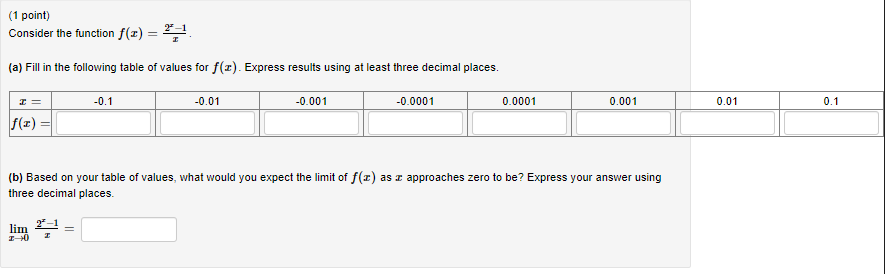
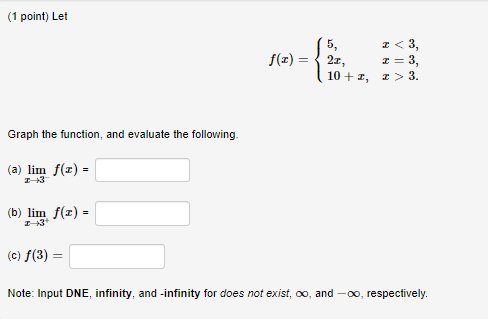
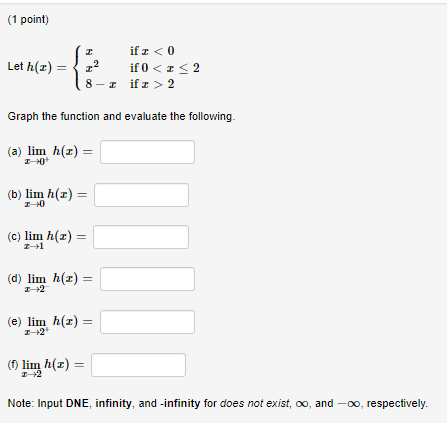
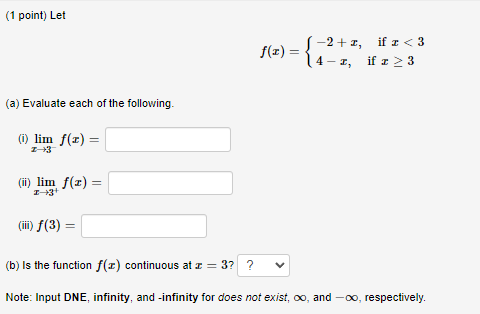
(1 point) Let F be the function whose graph is shown below. Evaluate each of the following. Note: Input DNE, infinity, and -infinity for does not exist, oo, and -oo, respectively. lim F(x)= 2. lim F(@)= 3, lim F()= 1 1 4. F(-1)= 110 5. lim F(x)= 1.0 lim F(x)= -3 5 6. T 7. lim F()= 8. lim F(@)= -I- 9. F(3)= -6 The graph of y = F(I).(1 point) Consider the function f(z) = -36 (a) Fill in the following table of values for f(X). Express results using at least three decimal places, where necessary. 5.9 5.99 5.999 5.9999 6.0001 6.001 6.01 6.1 f(I) (b) Based on your table of values, what would you expect the limit of f(@) as x approaches 6 to be? Express your answer to the nearest whole number. lim -36 I-6(1 point) Consider the function f () = 3-1 (a) Fill in the following table of values for f (&). Express results using at least three decimal places. -0.1 -0.01 -0.001 -0.0001 0.0001 0.001 0.01 0.1 f(I) (b) Based on your table of values, what would you expect the limit of f (c) as c approaches zero to be? Express your answer using three decimal places. lim(1 point) Let 5, f(I) = 21. 10+ I, = > 3. Graph the function, and evaluate the following (a) lim f(E) = (b) lim f(:) = (C) f (3) = Note: Input DNE, infinity, and -infinity for does not exist, oo, and -oo, respectively.(1 point) ife > 2 Graph the function and evaluate the following. (a) lim h(c) = (b) lim h(@) = (c) lim h(E) = I-+1 (d) lim h(E) = T 12 (e) lim h(I) = (0) lim h (x) = Note: Input DNE, infinity, and -infinity for does not exist, oo, and -oo, respectively.(1 point) Let -2+1, ife 3 (a) Evaluate each of the following. (i) lim f(x) = (ii) lim f(E) = (ii) f (3) = (b) Is the function f(x ) continuous at c = 3? ? Note: Input DNE, infinity, and -infinity for does not exist, oo, and -oo, respectively