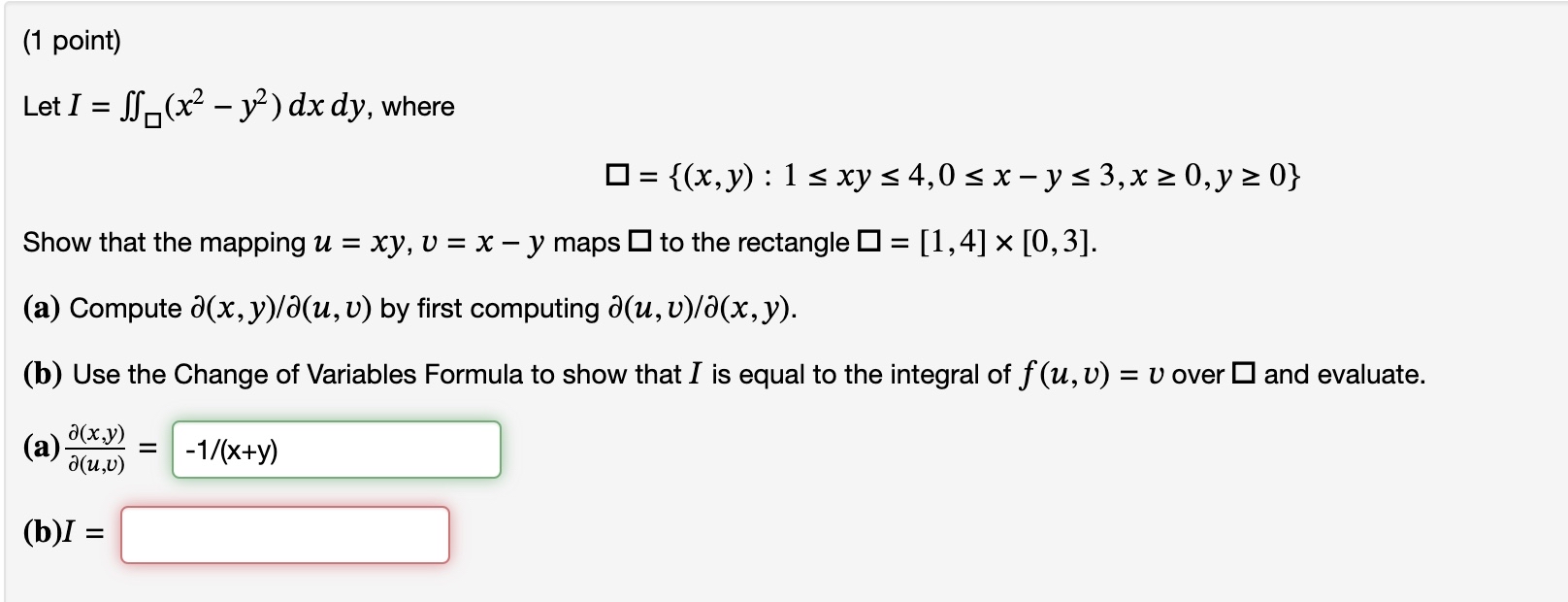
$(1$ point$)$

Let $I={}_{}(x^2-y^2)dxdy,$ where

$=\{(x,y)$:$1xy4,0x-y3,x0,y0\}$

Show that the mapping $u=xy,v=x-y$ maps $$ to the rectangle $=[1,4][0,3].$

$($a$)$ Compute del$\frac{x,y}{d}el(u,v)$ by first computing del$\frac{u,v}{d}el(x,y).$

$($b$)$ Use the Change of Variables Formula to show that I is equal to the integral of $f(u,v)=v$ over $$ and evaluate.

$($a$)\frac{\text{d}\text{e}\text{l}(x,y)}{\text{d}\text{e}\text{l}(u,v)}=$

$($b$)I=$