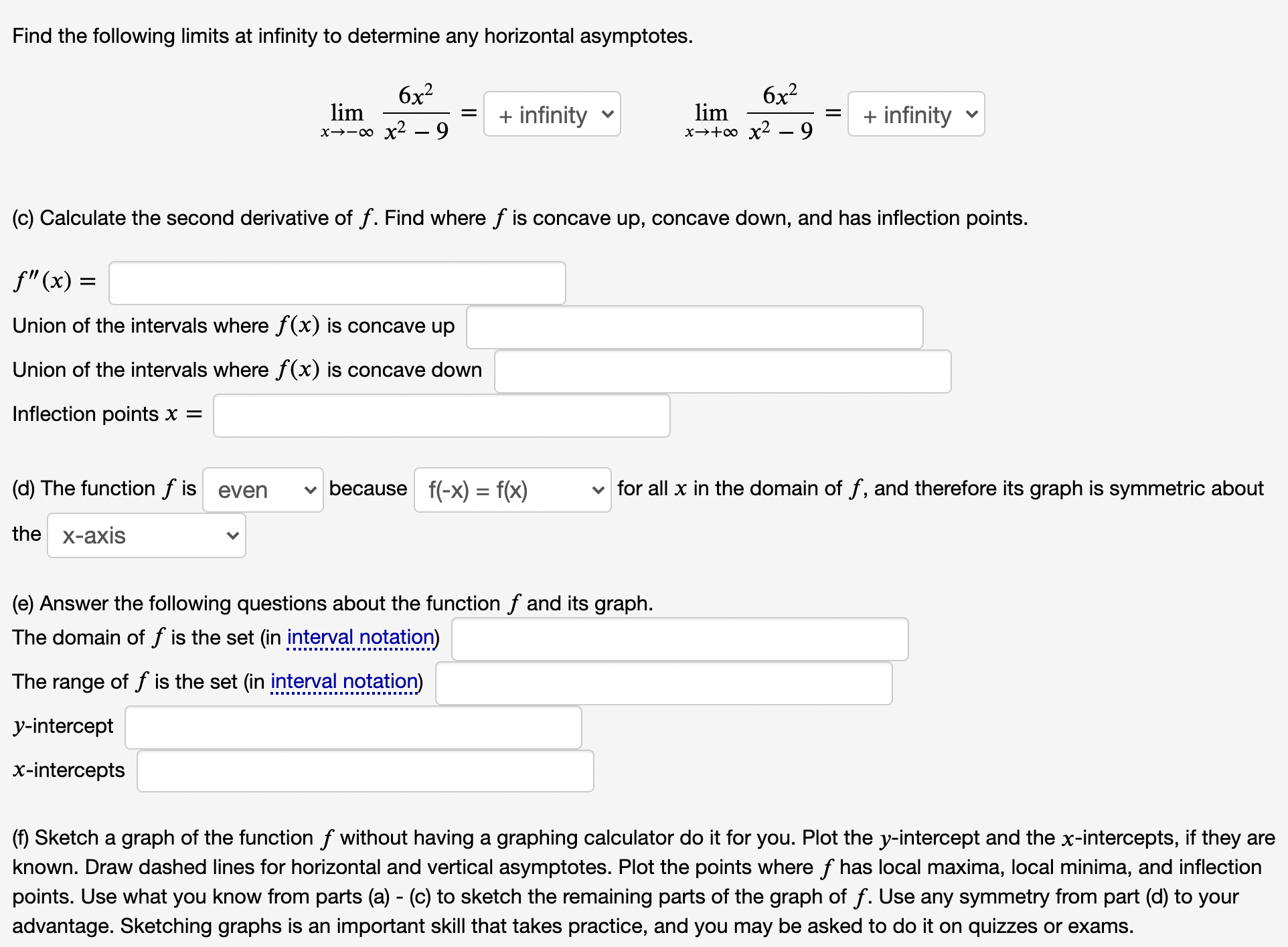
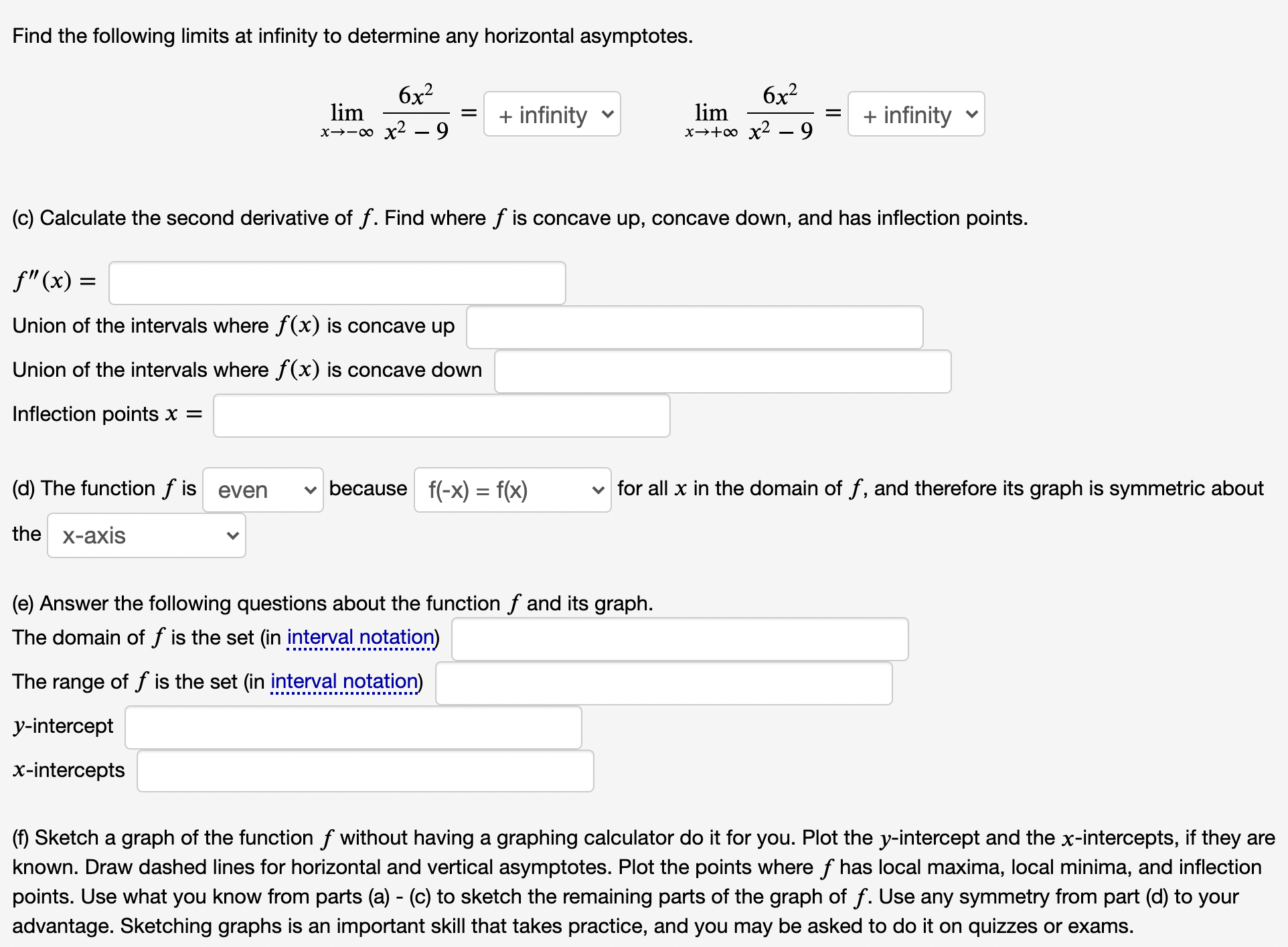
(1 point) Please answer the following questions about the function 6x2 f(x) =. x2 - 9 Instructions: . If you are asked for a function, enter a function. . If you are asked to find x- or y-values, enter either a number or a list of numbers separated by commas. If there are no solutions, enter None. . If you are asked to find an interval or union of intervals, use interval notation. Enter { } if an interval is empty. . If you are asked to find a limit, enter either a number, I for co, -| for -co, or DNE if the limit does not exist. (a) Calculate the first derivative of f. Find the critical numbers of f, where it is increasing and decreasing, and its local extrema. f' ( x) = Critical numbers x = Union of the intervals where f(x) is increasing Union of the intervals where f(x) is decreasing Local maxima x = Local minima x = (b) Find the following left- and right-hand limits at the vertical asymptote x = -3. 6x2 6x2 lim + infinity v lim = 6 x - - 3- x2 - 9 x--3+ x2 - 9 Find the following left- and right-hand limits at the vertical asymptote x = 3. 6x2 6x2 lim = 6 lim = x-3- X2 - - 9 + infinity v x-3+ x2 - 9Find the following limits at infinity to determine any horizontal asymptotes. lim 6x2 - r- - 1' 6x2 = V 1m x_)_m x2 _ + In Inlty \"+00 x2 _ 9 = + infinity v (c) Calculate the second derivative of f. Find where f is concave up, concave down, and has inflection points. f \" (x) = Union of the intervals where f (x) is concave up Union of the intervals where f (x) is concave down Inflection points x = (d) The function f is even v because f(-x) = f(x) v for all x in the domain of f, and therefore its graph is symmetric about the x-axis v (e) Answer the following questions about the function f and its graph. The domain of f is the set (in inlsmalnelatiel The range of f is the set (in intervalungtatiop) y-intercept x-intercepts (f) Sketch a graph of the function f without having a graphing calculator do it for you. Plot the yintercept and the x-intercepts, if they are known. Draw dashed lines for horizontal and vertical asymptotes. Plot the points where f has local maxima, local minima, and inflection points. Use what you know from parts (a) - (c) to sketch the remaining parts of the graph of f. Use any symmetry from part (d) to your advantage. Sketching graphs is an important skill that takes practice, and you may be asked to do it on quizzes or exams