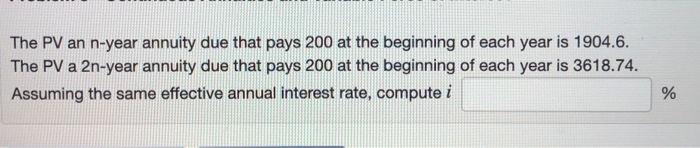
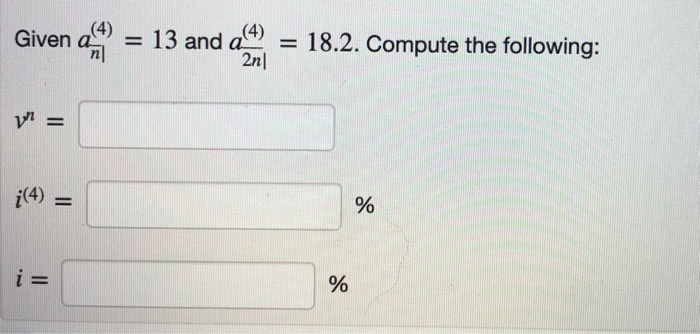
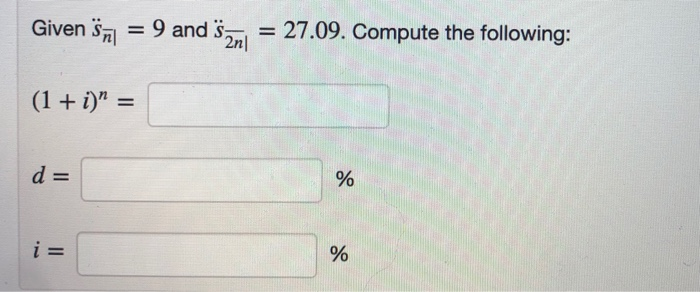
(1 point) Problem 3 - Continuous Annuities and Variable Force of interest Given the accumulation function a(t) = 1 + 0.061?. calculate the accumulated value at time 4 of four deposits of 400 at times 1,2,3,4. AV = Given an annuity immediate that pays 400 at the end of each year for 6 years. Use the accumulation function a(t) = 1 + 0.021 to calculate a) The present value of this annuity at time 0. PV = b) The accumulated value at time 6 of this annuity. AV = The PV an n-year annuity due that pays 200 at the beginning of each year is 1904.6. The PV a 2n-year annuity due that pays 200 at the beginning of each year is 3618.74. Assuming the same effective annual interest rate, compute i Problem 6 - Continuous Annuities and Variable Force of Interest Find the PV of a 12-year annuity with continuous payments at the rate of $ 470 a year at a force of interest 8 = 4.37%. PV = (1 point) Problem 7 - Continuous Annuities and Variable Force of Interest Given an annual effective rate of interest 4.9%, find the AV of a 9-year annuity with continuous payments at the rate of $ 5000 a year at time 14. (Note that the payments stop at time 9 but the balance still accumulate interest till time 14.) AV = 3.2. Compute the following: in = (4) = Given Sn = 9 and Sami = 27.09. Compute the following: (1 + i)" = d= i= (1 point) Problem 10 - Continuous Annuities and Variable Force of Interest Given an anual effective rate of interest i = 5.19%, compute the following: (1 point) Problem 3 - Continuous Annuities and Variable Force of interest Given the accumulation function a(t) = 1 + 0.061?. calculate the accumulated value at time 4 of four deposits of 400 at times 1,2,3,4. AV = Given an annuity immediate that pays 400 at the end of each year for 6 years. Use the accumulation function a(t) = 1 + 0.021 to calculate a) The present value of this annuity at time 0. PV = b) The accumulated value at time 6 of this annuity. AV = The PV an n-year annuity due that pays 200 at the beginning of each year is 1904.6. The PV a 2n-year annuity due that pays 200 at the beginning of each year is 3618.74. Assuming the same effective annual interest rate, compute i Problem 6 - Continuous Annuities and Variable Force of Interest Find the PV of a 12-year annuity with continuous payments at the rate of $ 470 a year at a force of interest 8 = 4.37%. PV = (1 point) Problem 7 - Continuous Annuities and Variable Force of Interest Given an annual effective rate of interest 4.9%, find the AV of a 9-year annuity with continuous payments at the rate of $ 5000 a year at time 14. (Note that the payments stop at time 9 but the balance still accumulate interest till time 14.) AV = 3.2. Compute the following: in = (4) = Given Sn = 9 and Sami = 27.09. Compute the following: (1 + i)" = d= i= (1 point) Problem 10 - Continuous Annuities and Variable Force of Interest Given an anual effective rate of interest i = 5.19%, compute the following