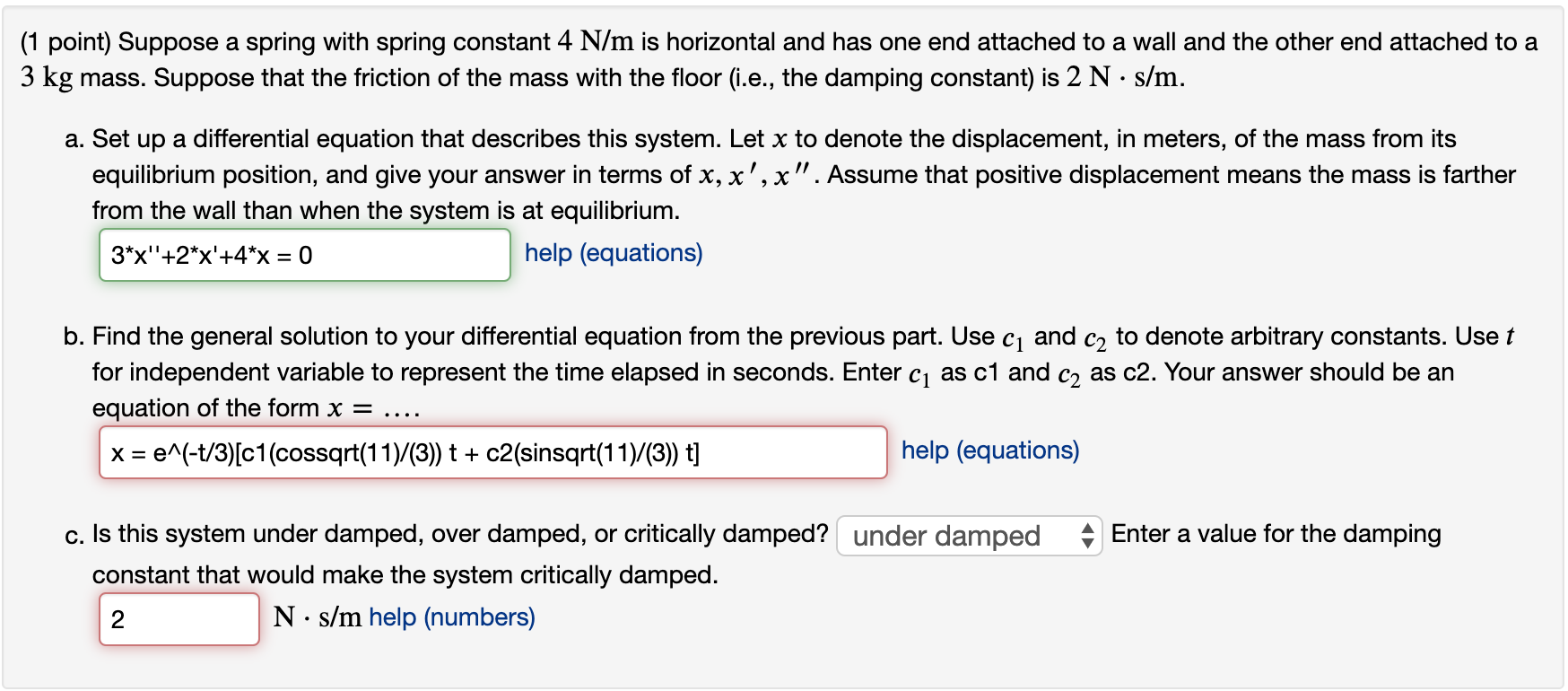
(1 point) Suppose a spring with spring constant 4 N/m is horizontal and has one end attached to a wall and the other end attached to a 3 kg mass. Suppose that the friction of the mass with the floor (i.e., the damping constant) is 2 N s/m. a. Set up a differential equation that describes this system. Let x to denote the displacement, in meters, of the mass from its equilibrium position, and give your answer in terms of x, x',x". Assume that positive displacement means the mass is farther from the wall than when the system is at equilibrium. 3*x"+2*x'+4*x = 0 help (equations) b. Find the general solution to your differential equation from the previous part. Use cy and cz to denote arbitrary constants. Use t for independent variable to represent the time elapsed in seconds. Enter c as c1 and c2 as c2. Your answer should be an equation of the form x = .. x = e^(-t/3)[c1(cossqrt(11)/(3)) t + c2(sinsqrt(11)/(3)) t] help (equations) Enter a value for the damping c. Is this system under damped, over damped, or critically damped? under damped constant that would make the system critically damped. 2 N s/m help (numbers)