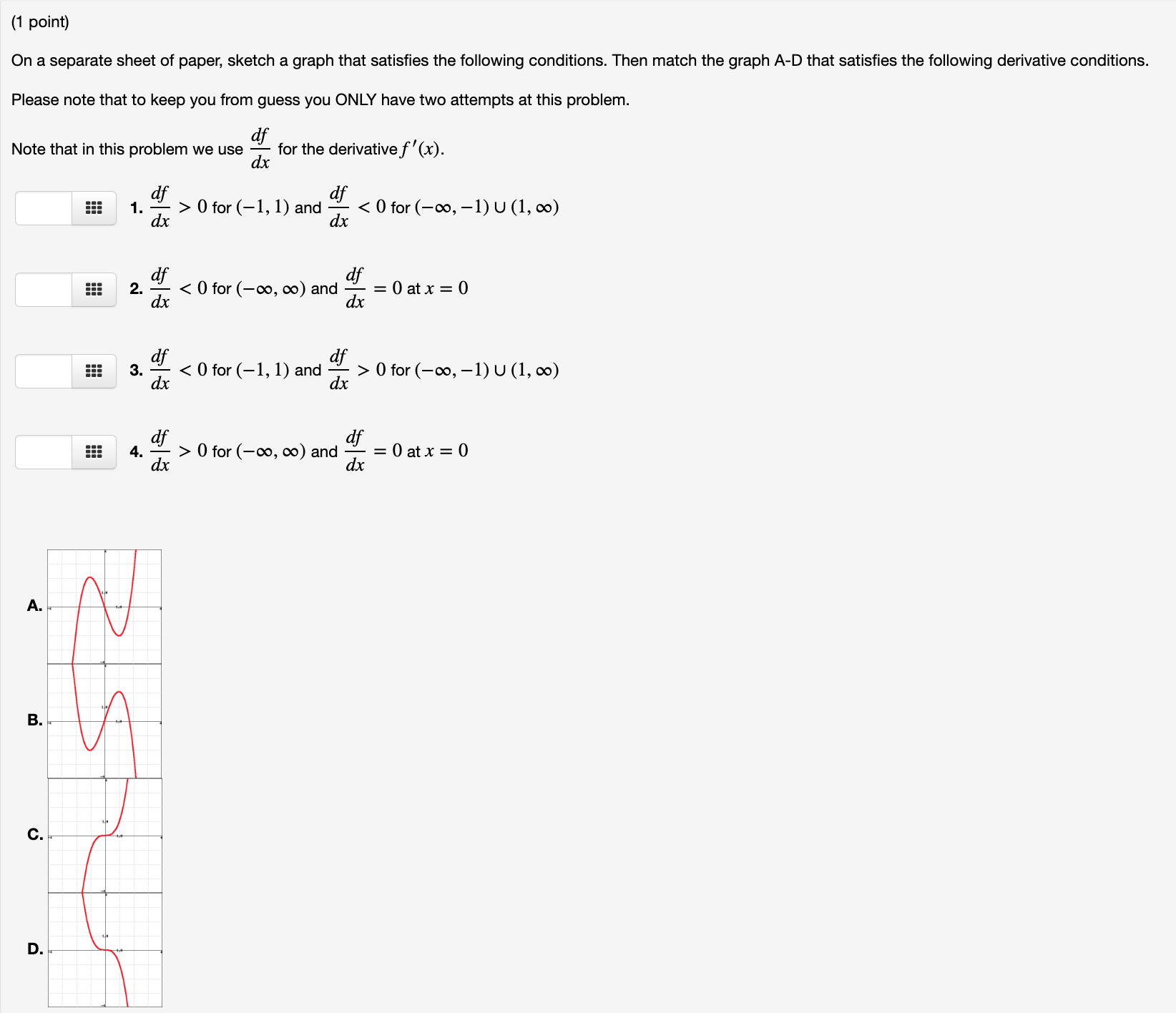
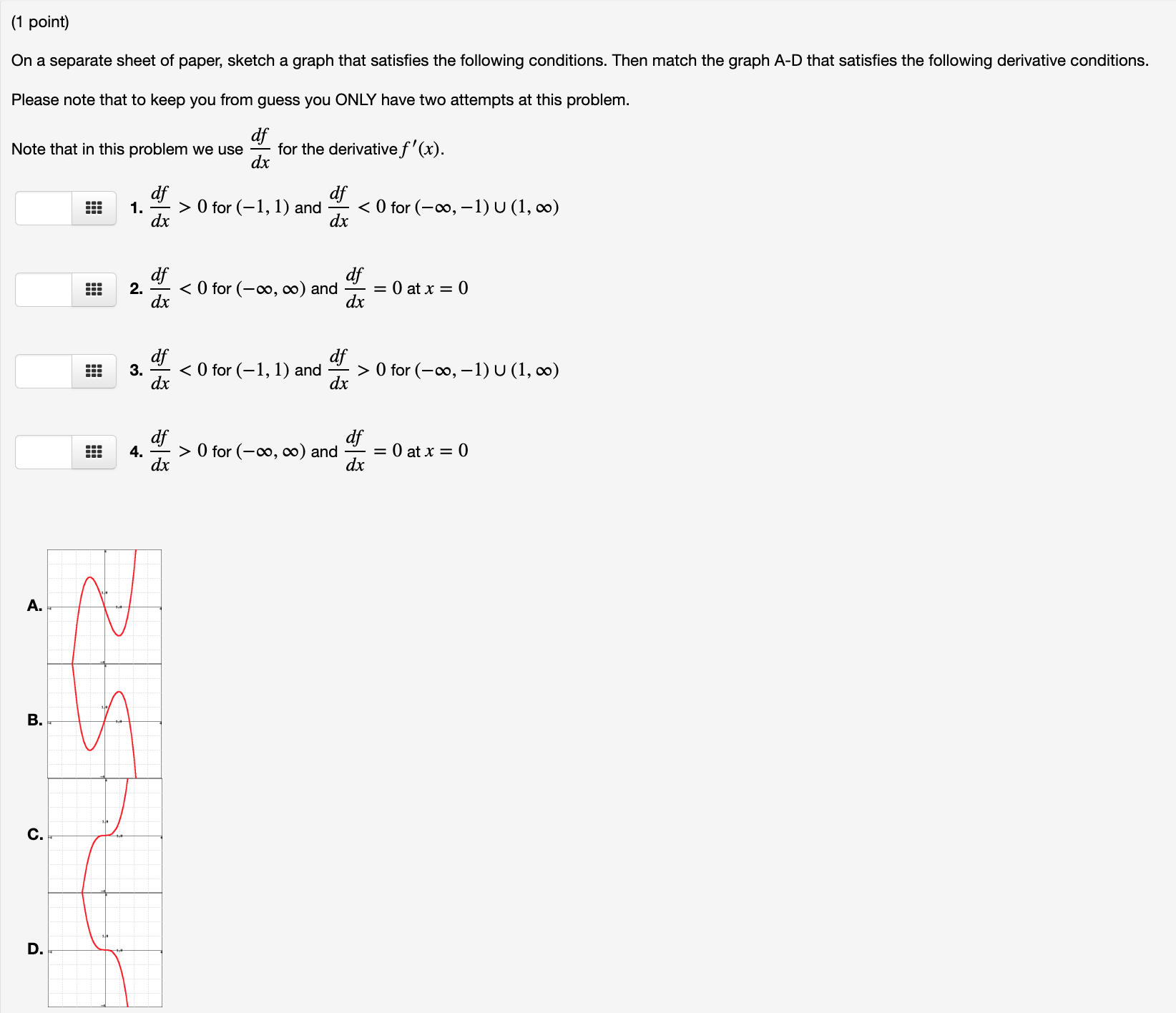
(1 point) Suppose that it is known that the second derivative of f(x) factors as f\"(x) = 7(x + 2)(x 13)2(x 10). Find the largest open intervals for which f (x) is concave up. Find the largest open intervals for which f (x) is concave down. Concave up :2 Concave down 555 Find the x values for all inflection points of the graph of y = f(x). lnflection points at x = Suppose in addition, it is known that f ' (0) = 0. According to the Second Derivative Test, can we say anything about whether f(x) has a relative maximum or relative minimum at x = 0? We can conclude that O A.f(x) has a relative maximum atx = 0 sincef(x) is concave down at): = 0. O B. f(x) has a relative maximum at): = 0 since f(x) is concave up at x = 0. O c.f(x) has a relative minimum at): = 0 since f(x) is concave up at x = 0. O D. f(x) has a relative minimum at x = 0 since f(x) is concave down at x = 0. O E.f(x) has neither a relative maximum nor a relative minimum at x = 0. {1 point) A company manufacturers and sells x electric drills per month. The monthly cost and price-demand equations are C(x) = 63000 + 80x. p(x)=190 %, 0 Sx 55000. (A) Find the production level that results in the maximum revenue. Production Level = :== (E) Find the production level that results in the maximum prot. Number of drills = 5!! (C) Find the price that the company should charge for each drill in order to maximize prot. Price = :== (1 point) On a separate sheet of paper, sketch a graph that satisfies the following conditions. Then match the graph A-D that satisfies the following derivative conditions. Please note that to keep you from guess you ONLY have two attempts at this problem. Note that in this problem we use dx " for the derivative f' (x) . 1 . > 0 for (-1, 1) and 0 for (-co, -1) U (1, co) 4. - dif dx > 0 for (-0o, co) and - = 0 at x = 0 A. $5 2 C. D