Question: (1 point) Suppose the sequence a(n) satisfies the following linear recurrence: a(n) = 6a(n 1) +5; a(0) = 6. (a) Find a closed (explicit)

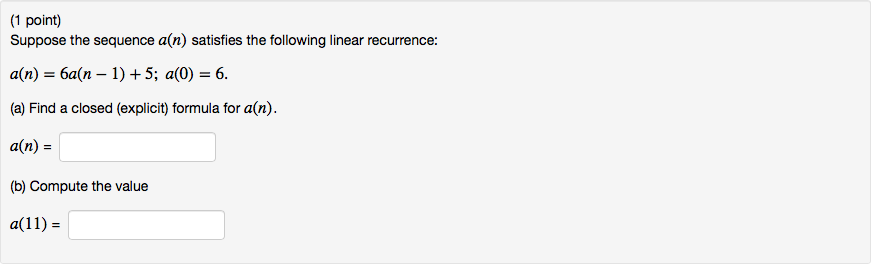
(1 point) Suppose the sequence a(n) satisfies the following linear recurrence: a(n) = 6a(n-1) + 5; a(0) 6. (a) Find a closed (explicit) formula for a(n) a(n) = (b) Compute the value a(11)

(1 point) Suppose the sequence a(n) satisfies the following linear recurrence: a(n) = 6a(n 1) +5; a(0) = 6. (a) Find a closed (explicit) formula for a(n). a(n) = (b) Compute the value a(11) =

Step by Step Solution

★★★★★

3.40 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To solve this problem well follow these steps a Find a closed explicit formula for an The given recu... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Find the explicit formula for the general solution to the linear iterative systems with the following coefficient matrices: (a) (b) (c) (d) 3 21 235 246 362 16 1-3 243

Find an explicit formula for f 1and use it to graph f 1, f and the line y = x on the same screen. To check your work, see whether the graphs of f and f 1 are reflections about the line. 29. f(x) = 1...

Find an explicit formula for f (n) if f (1) = 1 and f (n) = f (n 1) + 2n 1 for n 2. Prove your result using mathematical induction.

The excel homework assignment below has five tabs that cover five different topics: Net Present Value Analysis, Capital Budgeting and Cost of Capital, Working Capital, Management, Financial Ratio...

Math 2211 3.5-3.10 Review Name _________________________ Just Relax and Think Positively!!!! I Know you CAN Do This!!! 1. Let () = 1 . Find the value of (1). 2. Let () = 1 2. Find the value of (0)....

INSTRUCTIONS: 1) Do all necessary steps 2) This is a whole paper. No data is missing. 1. SYSTEMS OF LINEAR EQUATIONS 1.2. Exercises (1) Suppose that In and Ly are lines in the plane, that the...

Please reply to the following attachments provided below. (1 point) Find the least-squares regression line y = bo + biz through the points (-1,0), (0, 6), (6, 13), (9, 18), (11, 26) For what value of...

QUESTION 1 Which of the following descriptions of confidence interval is correct? if) A. If a 95% confidence interval contains 0. then the 90% confidence interval contains 0 CT;- 9. If a 95%...

Fixed Capital (Current U.S. Dollars) Labor Force GDP (Current U.S. Dollars) K Country Name L Y Afghanistan 2,190,816,336.48 8,720,341.85 14,213,670,485.31 Albania 3,489,305,719.30 1,478,120.92...

This is my Powerpoint from my class that talks about Predicted Values. I know the answer is 2 , but I don't know how to get the correct answer. I hope this helps. . I need some help with this one. I...

Explain An example of a physical control the client can use to protect each of the following assets or records is, Petty cash should be kept locked in a fireproof safe

12. Eveline is reading a news article and comes across a shocking statistic in an online news article that says, "87% of all frogs are poisonous if you lick them." This statistic doesn't sound right,...

Given a set S of integers, an integer total, and a non-negative integer budget, the SubsetSum Decision problem is to report whether or not there is a subset of S, containing at most budget elements,...

Given the contents of the receipt.txt file; write a series of piped commands that will read the file and output a count of the number of lines that contain a negative number. receipt.txt Burrito...

The Secretary of the Interior recently announced the creation of the "Bring Waldo Home" project. When asked if this project was justified he responded that it would create over 8,000 jobs. Explain...

A new member of an agile development team believes it is unfair to track defect counts at the team level when the continuous integration tool identifies the developer associated with each logged...

Given below is the interest coverage ratio for each credit slab and the corresponding spread over the risk free rate (5%) for large manufacturing firms. Interest Coverage Ratio Cr. Rating Spread...

Suppose the spot and six-month forward rates on the Norwegian krone are Kr 5.78 and Kr 5.86, respectively. The annual risk-free rate in the United States is 3.8 percent, and the annual risk-free rate...

Use the Gram-Schmidt process based on the L2 inner product on [0, 1] to construct a system of orthogonal polynomials of degree

Prove that the Jacobi identity [[A, B]. C] + ([C. A], B] -([[B, C], A] = O is valid for any three n x n matrices.

(b) Which pairs of the elementary matrices listed in (1.19) commute? (c) Can you formulate a general rule that tells in advance whether two given elementary matrices commute?

Families USA, a monthly magazine that discusses issues related to health and health costs, surveyed 20 of its subscribers. It found that the annual health insurance premiums for a family with...

Ms. Maria Wilson is considering running for mayor of the town of Bear Gulch, Montana. Before completing the petitions, she decides to conduct a survey of voters in Bear Gulch. A sample of 400 voters...

The Fox TV network is considering replacing one of its prime-time crime investigation shows with a new family-oriented comedy show. Before a final decision is made, network executives commission a...