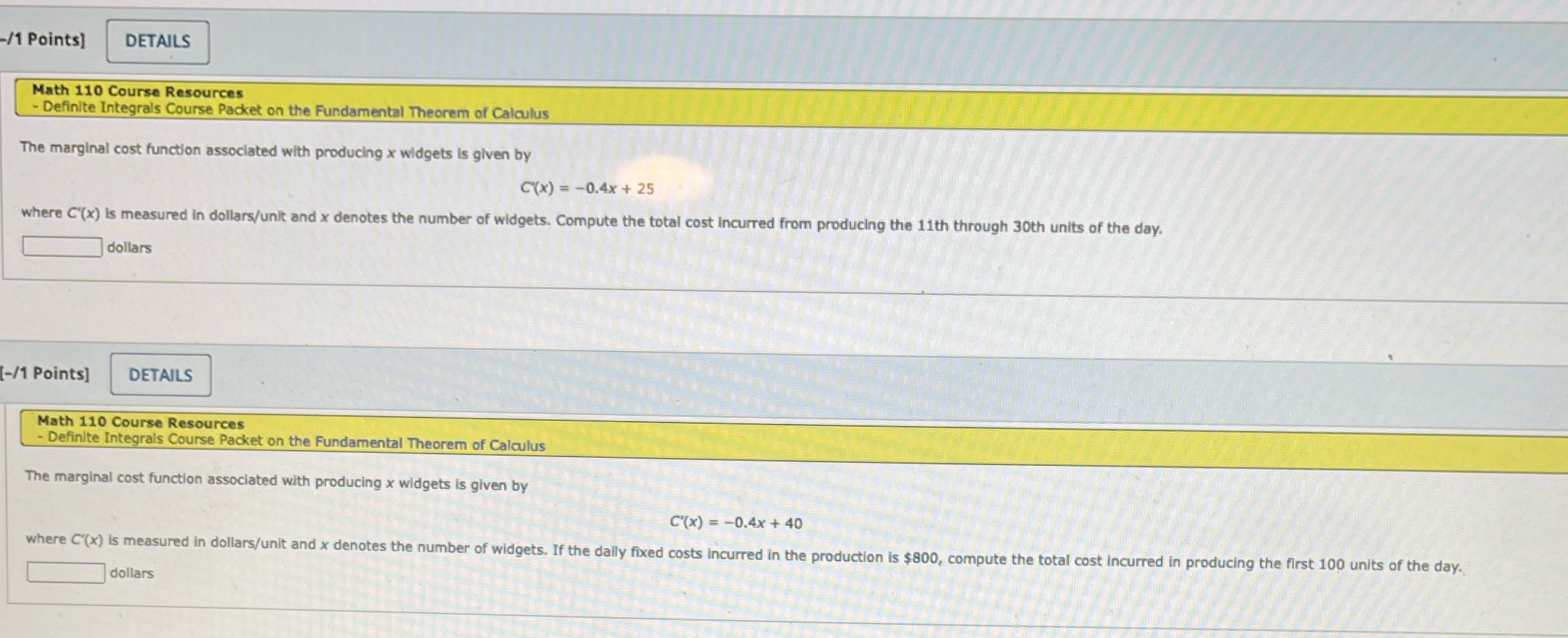
/1 Points] DETAILS Math 110 Course Resources Definite Integrals Course Packet on the Fundamental Theorem of Calculus The marginal cost function associated with producing x widgets is given by (x) = -0.4x + 25 where C'(x) is measured in dollars/unit and x denotes the number of widgets. Compute the total cost Incurred from producing the 11th through 30th units of the day. dollars -/1 Points] DETAILS Math 110 Course Resources - Definite Integrals Course Packet on the Fundamental Theorem of Calculus The marginal cost function associated with producing x widgets is given by C'(x) = -0.4x + 40 where C'(x) is measured in dollars/unit and x denotes the number of widgets. If the dally fixed costs incurred in the production is $800, compute the total cost incurred in producing the first 100 units of the day. dollars