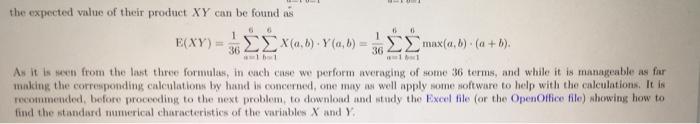1. (Random Variables Standard Numerical Characteristics: Joint Distributions). Let a pair of fair four-faced dice be tossed. Consider the random variables X,Y:S-R on the corresponding sample space defined by X(a, b) = max(a, b). Y(a,b) =a + b where (a,b) runs over S {1,2,3,4} {1,2,3,4). Find the joint distribution (x,y) of X and Y. (1) Use (1) to find the marginal distributions f(x) and g() asociated with the joint distribution (x). () Use () to find E(X). E(X), Var(x), and ox (iv) Use (ii) to find ELY), E(Y), Var(Y), and ay: (v) Use (1) to find the expected value E(XY) of the product X. Y of X and Y (vi) Use (v). (1), and (iv) to find the covariance Cov(X,Y) of X and Y. (vii) Use (vi), (i), and (iv) to find the correlation (X,Y) of X and Y. Please give a complete, fully typed, solution to the problem. It can be proven that given a random variable X: S - R on a finite probability space S, in addition to the standard formula E(X)= P(X = ?), 6X(8) for the expected value E(X) of X, one can use the formula E(X) - (0) ) (5.1) BES 1 ES (the proof will be discussed during the forthcoming lecture). As a corollary we obtain that if S is a finite equiprobable space, then E(X)= (6) = 2.5 X(s) (5.2) IS observe that, in effect, the expected value of X is then simply the average of all values X(), where s runs over S. Generally, the formula (5.1) can be used if the distribution f(x) = P(X). [+ X(S)] of X is either hard to come by, or unnecessary, etc. Furthermore, it should be pointed out that if the cardinality of S is large enough, the calculations based on the formula (5.1) may be quite involved to performa by band, For instance, by (5.2), the expected value of any random variable 2 SR on the probability space S = {(6) : a, b = 1,2....,6) associated with the experiment "tossing two fair dice" (of cardinality S1 = 36) can be found as ) ) SI EZ) 1 2 (, ). In particular, the expected values of the random variables X ("maximum") and Y ("sum") on S. we have considered during the lectures, can be found with use of the formulas EX) = (, ) =, max(a, b) 36 36 and 6 6 EY) (a,b) - + ): 36 36 66 6 0 1 36 1 the expected value of their product XY can be found as EXY) (, ) - Y(, ) max(a,b) (a+b). 36 As it is een from the last three formules, in cach chee we perform averaging of some 36 terms, and while it is manageable as far making the corresponding calculations by hand in concerned, one may well apply some noftware to help with the calculations. It is recommended before proceeding to the next problem, to download and study the Excel file (or the OpenOffice file) showing how to find the standard numerical characteristics of the variables X and Y