$1.$ Set up an integral for and compute the volume of the solid formed by taking a region$/$base enclosed by $\backslash ($ y$=1-$x$^\{2\}\backslash )$ and the $\backslash ($ x $\backslash )-$axis. First, build the $3-$dimensional shape with cross sections parallel to the $\backslash ($ y $\backslash )-$axis from squares.

$(1)$ Draw a diagram of the base and some sample squares to the best of your ability.

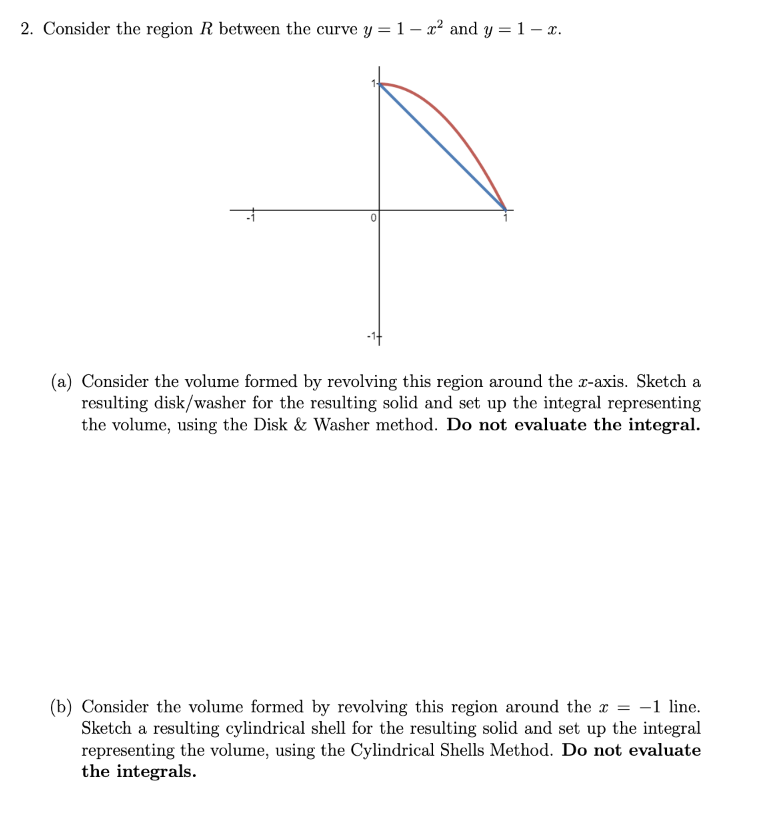
$(2)$ Set up the integral for the volume. $(3)$ Evaluate the integral, showing all work. $2.$ Consider the region $\backslash ($ R $\backslash )$ between the curve $\backslash ($ y$=1-$x$^\{2\}\backslash )$ and $\backslash ($ y$=1-$x $\backslash ).$

$($a$)$ Consider the volume formed by revolving this region around the $\backslash ($ x $\backslash )-$axis. Sketch a resulting disk$/$washer for the resulting solid and set up the integral representing the volume, using the Disk $\backslash$& Washer method. Do not evaluate the integral.

$($b$)$ Consider the volume formed by revolving this region around the $\backslash ($ x$=-1\backslash )$ line. Sketch a resulting cylindrical shell for the resulting solid and set up the integral representing the volume, using the Cylindrical Shells Method. Do not evaluate the integrals.