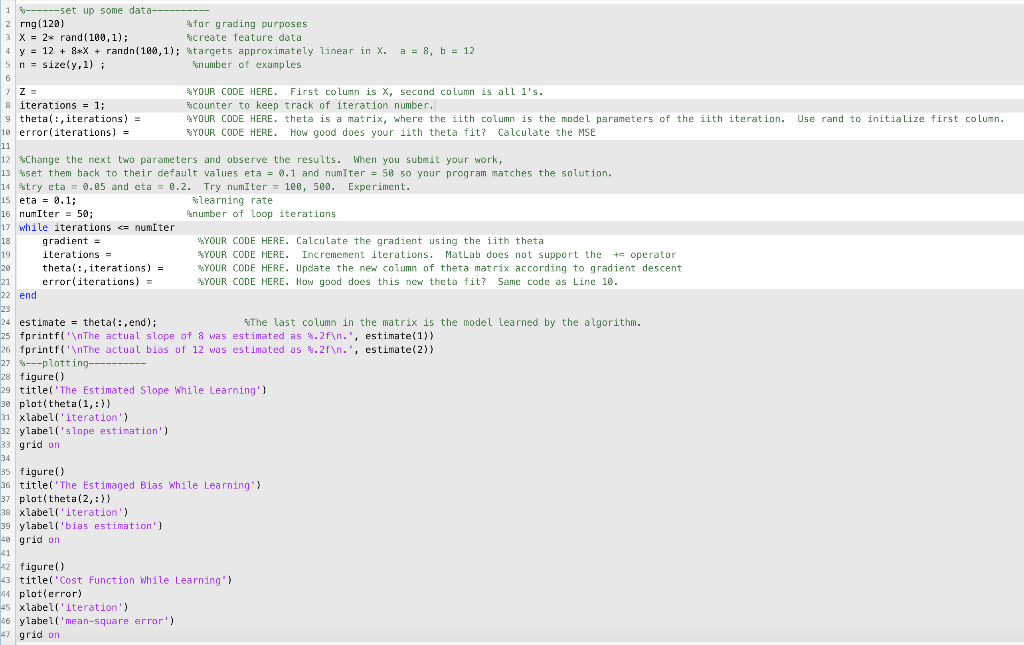
1 ------set up some data------ 2 rng(120) for grading purposes 3 X = 2* rand(100,1); Bcreate feature data 4 y = 12 + 8*X + randn(180,1); $targets approximately linear in X. 5 n = size(y, 1); number of examples a = a, b = 12 8 iterations = 1; 9 thetal:, iterations) = 10 error(iterations) = YOUR CODE HERE. First column is X, second column is all l's. counter to keep track of iteration number. %YOUR CODE HERE. theta is a matrix, where the iith column is the model parameters of the iith iteration. Use rand to initialize first column. RYOUR CODE HERE. How good does your lith theta fit? Calculate the MSE 12 Change the next two parameters and observe the results. When you submit your work, 13 set them back to their default values eta = 0.1 and numiter = 50 50 your program matches the solution. 14 try eta = 0.65 and eta = 8.2. Try numiter = 180, 580. Experiment. 15 eta = 0.1; learning rate 16 numIter = 50; number of loop iterations 17 while iterations = numiter gradient = YOUR CODE HERE. Calculate the gradient using the iith theta iterations = YOUR CODE HERE. Incremement iterations. MatLab does not support the += operator theta(:, iterations) = YOUR CODE HERE. Update the new column of theta matrix according to gradient descent error(iterations) = YOUR CODE HERE. How good does this new theta fit? Same code as Line 10. 22 end 24 estimate = thetal: , end); The last column in the matrix is the model learned by the algorithm. 25 fprintf(' The actual slope of 8 was estimated as 4.2f .', estimate(1) 26 fprintf(' The actual bias of 12 was estimated as .2f .', estimate(2)] 27 ---plotting------ 28 figure() 29 title('The Estimated Slope While Learning' 30 plot(theta(1,:)) 31 xlabell'iteration') 32 ylabel('slope estimation') 33 grid on 35 figure() 36 title('The Estimaged Bias While Learning' 37 plot(theta(2,:)) 38 xlabell'iteration') 39 ylabel('bias estimation') 40 grid on 42 figure() 43 title('Cost Function while Learning' 44 plot(error) 45 xlabell'iteration') 46 ylabel('mean-square error') 47 grid on The script below begins by generating a 1-D dataset that is approximately linear, with slope 8 and bias 12. You will complete the script by estimating the model parameters with the method of gradient descent. Recall that the cost function we wish to minimize in linear regression is the mean-square error (MSE). The gradient of the MSE, given estimate 0, is dJ = 2 (Z+Ze Zy), [ d n where Zis the usual data matrix augmented with ones, and y is the training target vector of length n. Also, recall the update equation in gradient descent for 0 is where n the learning rate. Finish the code to implement gradient descent. When you are finished, go back and change algorithm hyperparameters eta and numIter, and observe the effect they have on the results. 1 ------set up some data------ 2 rng(120) for grading purposes 3 X = 2* rand(100,1); Bcreate feature data 4 y = 12 + 8*X + randn(180,1); $targets approximately linear in X. 5 n = size(y, 1); number of examples a = a, b = 12 8 iterations = 1; 9 thetal:, iterations) = 10 error(iterations) = YOUR CODE HERE. First column is X, second column is all l's. counter to keep track of iteration number. %YOUR CODE HERE. theta is a matrix, where the iith column is the model parameters of the iith iteration. Use rand to initialize first column. RYOUR CODE HERE. How good does your lith theta fit? Calculate the MSE 12 Change the next two parameters and observe the results. When you submit your work, 13 set them back to their default values eta = 0.1 and numiter = 50 50 your program matches the solution. 14 try eta = 0.65 and eta = 8.2. Try numiter = 180, 580. Experiment. 15 eta = 0.1; learning rate 16 numIter = 50; number of loop iterations 17 while iterations = numiter gradient = YOUR CODE HERE. Calculate the gradient using the iith theta iterations = YOUR CODE HERE. Incremement iterations. MatLab does not support the += operator theta(:, iterations) = YOUR CODE HERE. Update the new column of theta matrix according to gradient descent error(iterations) = YOUR CODE HERE. How good does this new theta fit? Same code as Line 10. 22 end 24 estimate = thetal: , end); The last column in the matrix is the model learned by the algorithm. 25 fprintf(' The actual slope of 8 was estimated as 4.2f .', estimate(1) 26 fprintf(' The actual bias of 12 was estimated as .2f .', estimate(2)] 27 ---plotting------ 28 figure() 29 title('The Estimated Slope While Learning' 30 plot(theta(1,:)) 31 xlabell'iteration') 32 ylabel('slope estimation') 33 grid on 35 figure() 36 title('The Estimaged Bias While Learning' 37 plot(theta(2,:)) 38 xlabell'iteration') 39 ylabel('bias estimation') 40 grid on 42 figure() 43 title('Cost Function while Learning' 44 plot(error) 45 xlabell'iteration') 46 ylabel('mean-square error') 47 grid on The script below begins by generating a 1-D dataset that is approximately linear, with slope 8 and bias 12. You will complete the script by estimating the model parameters with the method of gradient descent. Recall that the cost function we wish to minimize in linear regression is the mean-square error (MSE). The gradient of the MSE, given estimate 0, is dJ = 2 (Z+Ze Zy), [ d n where Zis the usual data matrix augmented with ones, and y is the training target vector of length n. Also, recall the update equation in gradient descent for 0 is where n the learning rate. Finish the code to implement gradient descent. When you are finished, go back and change algorithm hyperparameters eta and numIter, and observe the effect they have on the results