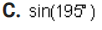
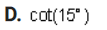
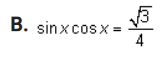
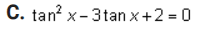
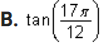
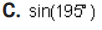
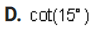
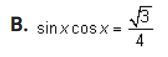
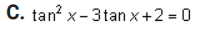
1. Show that this is an identity by using the definitions of the sum and difference formulas for cosine: sin a sin b = =[cos(a - b) - cos(a + b)] Complete the left-hand column of the table below following the steps indicated in the right-hand column. (12 points) Calculation Reason [cos(a - b) - cos(a+ b) ] Given on the right side of the original problem Apply the definitions of the sum and difference identities for cosine Simplify the expressions2. Use the subtraction formula for sine to verify this identity: sin X = COS X 2 Complete the two columns of the table below to demonstrate that this is an identity. (12 points) Calculation Reason Given on the left side of the sin X original problem3. Find the exact value of each of the following. Do not use a calculator - answers given as decimals will not receive credit. A. cos 7 x 12 Part I: Find two common angles that either add up to or differ by 7% Rewrite this 12 problem as the cosine of either a sum or a difference of those two angles. (2 points)Part II: Evaluate the expression. (4 points\fPart I: Find two common angles that either add up to or differ by 17 x Rewrite this 12 problem as the tangent of either a sum or a difference of those two angles. (2 points)Part II: Evaluate the expression. (4 points)\fPart I: Find two common angles that either add up to or differ by 195 . Rewrite this problem as the sine of either a sum or a difference of those two angles. (2 points)Part II: Evaluate the expression. (4 points\fPart I: Find two common angles that differ by 150 . Rewrite this problem as the cotangent of a difference of those two angles.(2 points)\f4. Rewrite sin* x so that it involves only the first power of cosine. Complete the two columns of the table below to demonstrate that this is an identity. (10 points) Calculation Reason sin* x Given in the problem5. Prove the identity: sin (2x) cos(2x) = sec x sin x COS X Complete the two columns of the table below to demonstrate that this is an identity. (12 points) Calculation Reason sin (2x) cos(2x) Given on the left side of the sin x COSX original problem6. Prove the identity: (cos x + cosy) + (sinx - siny} = 2+ 2cos(x + y) Complete the two columns of the table below to demonstrate that this is an identity. (12 points) Calculation Reason (cos x + cosy) + (sinx - siny) Given on the left side of the original problem7. Solve these equations: A. sin X+ - sin X- Part I: Apply the sum and difference formulas for sine to simplify the left-hand side of the equation. (2 points)Part II: Find a// solutions to the equation you found in part I. (4 points)\fPart I: Use the double-angle formula for sine to rewrite the problem in terms of sine only.(2 points)\fC. tar 3tan x +2 =Part I: Factor the expression in the equation to make it easier to solve.(2 points)Part II: Solve the equation, finding all solutions.(4 points)