1.)

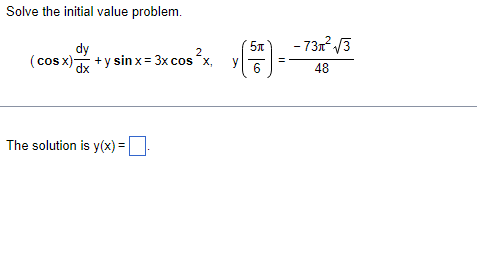
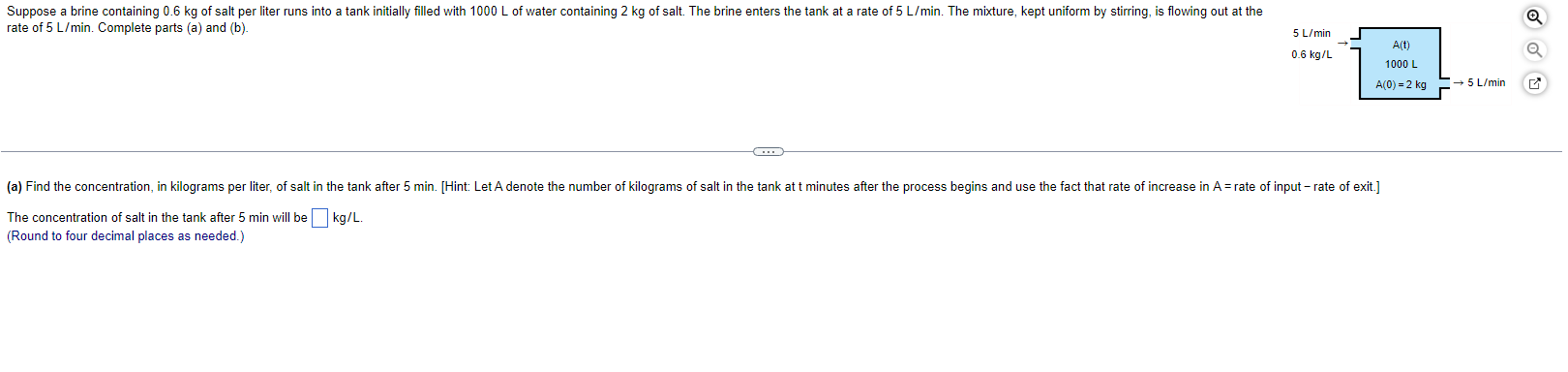
Solve the initial value problem. dx 3 + 2tx =t" Int+1, x(1)=0 dt The solution is x(t) =.Solve the initial value problem. dy 2 - 73x-13 ( cos x)- dx + y sin x = 3xcos X, 48 The solution is y(x) =A rock contains two radioactive isotopes, RA, and RA2, that belong to the same radioactive series; that is, RA, decays into RA2, which then decays into stable atoms. Assume that the rate at which RA, decays into RA2 is 50e" kg/sec. Because the rate of decay of RA2 is proportional to the mass y(t) of RA2 present, the rate of change in RA2 is as follows, where k > 0 is the decay constant. dy - = rate of creation - rate of decay, or My = 50e- 30t - ky If k = 4/sec and initially y(0) = 25 kg, find the mass y(t) of RA2 for t2 0. For t2 0, the mass of RA2 is y(t) =. (Type an exact answer.)Suppose a brine containing 0.6 kg of salt per liter runs into a tank initially filled with 1000 L of water containing 2 kg of salt. The brine enters the tank at a rate of 5 L/min. The mixture, kept uniform by stirring, is flowing out at the rate of 5 L/min. Complete parts (a) and (b). 5 L/min A(t) 0.6 kg/L 1000 L A(0) = 2 kg - 5 L/min (a) Find the concentration, in kilograms per liter, of salt in the tank after 5 min. [Hint: Let A denote the number of kilograms of salt in the tank at t minutes after the process begins and use the fact that rate of increase in A = rate of input - rate of exit.] The concentration of salt in the tank after 5 min will be kg/L. (Round to four decimal places as needed.)