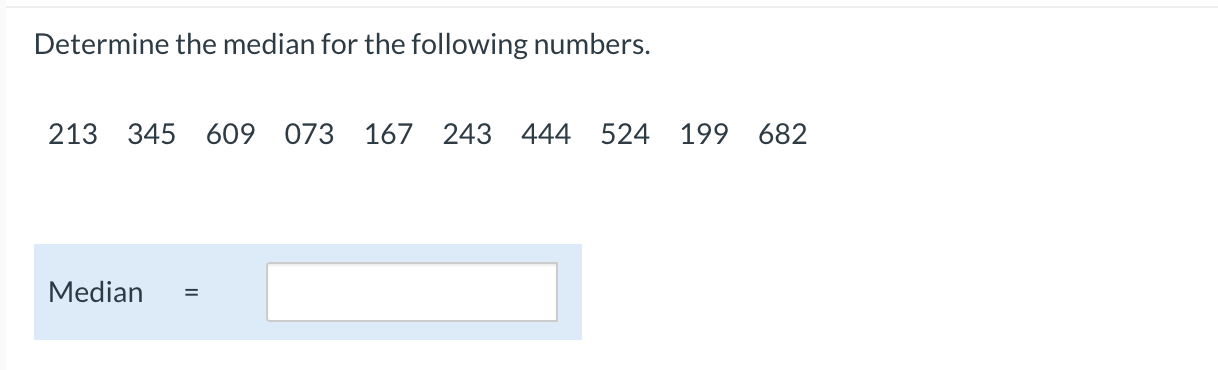
Question: 1) Some numbers are not normally distributed. If the mean of the numbers is 38 and the standard deviation is 6, what proportion of values


1)

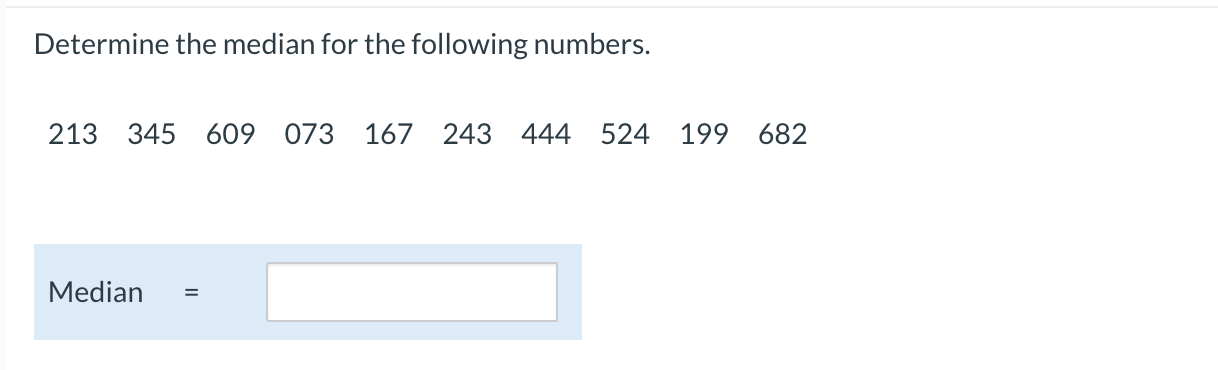
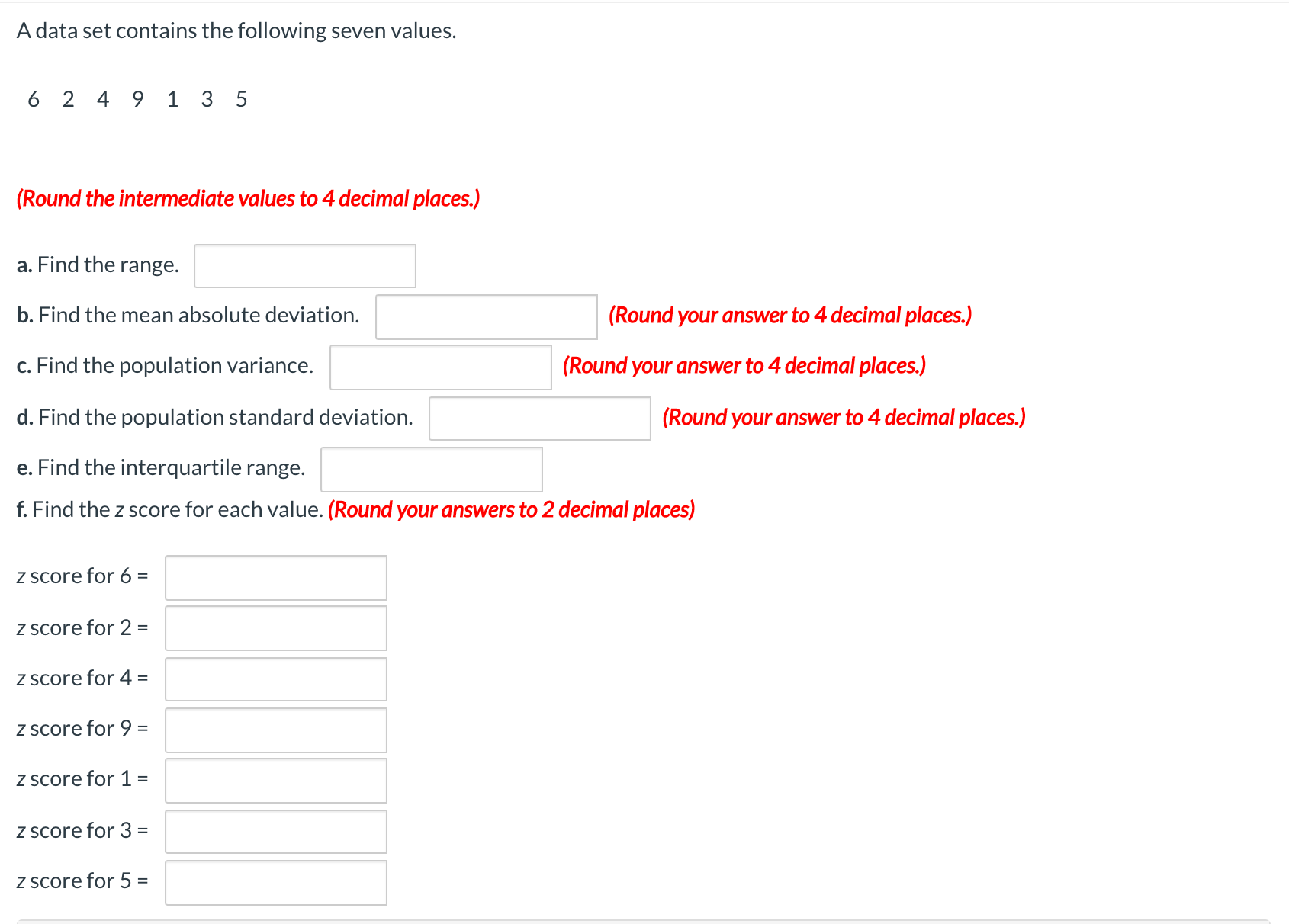

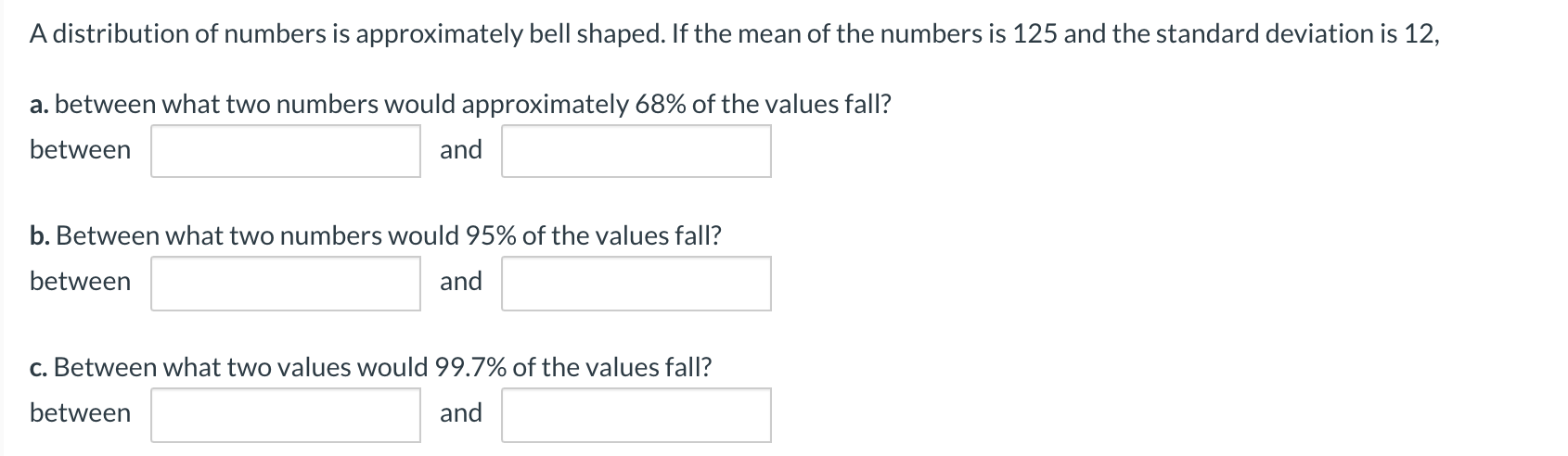
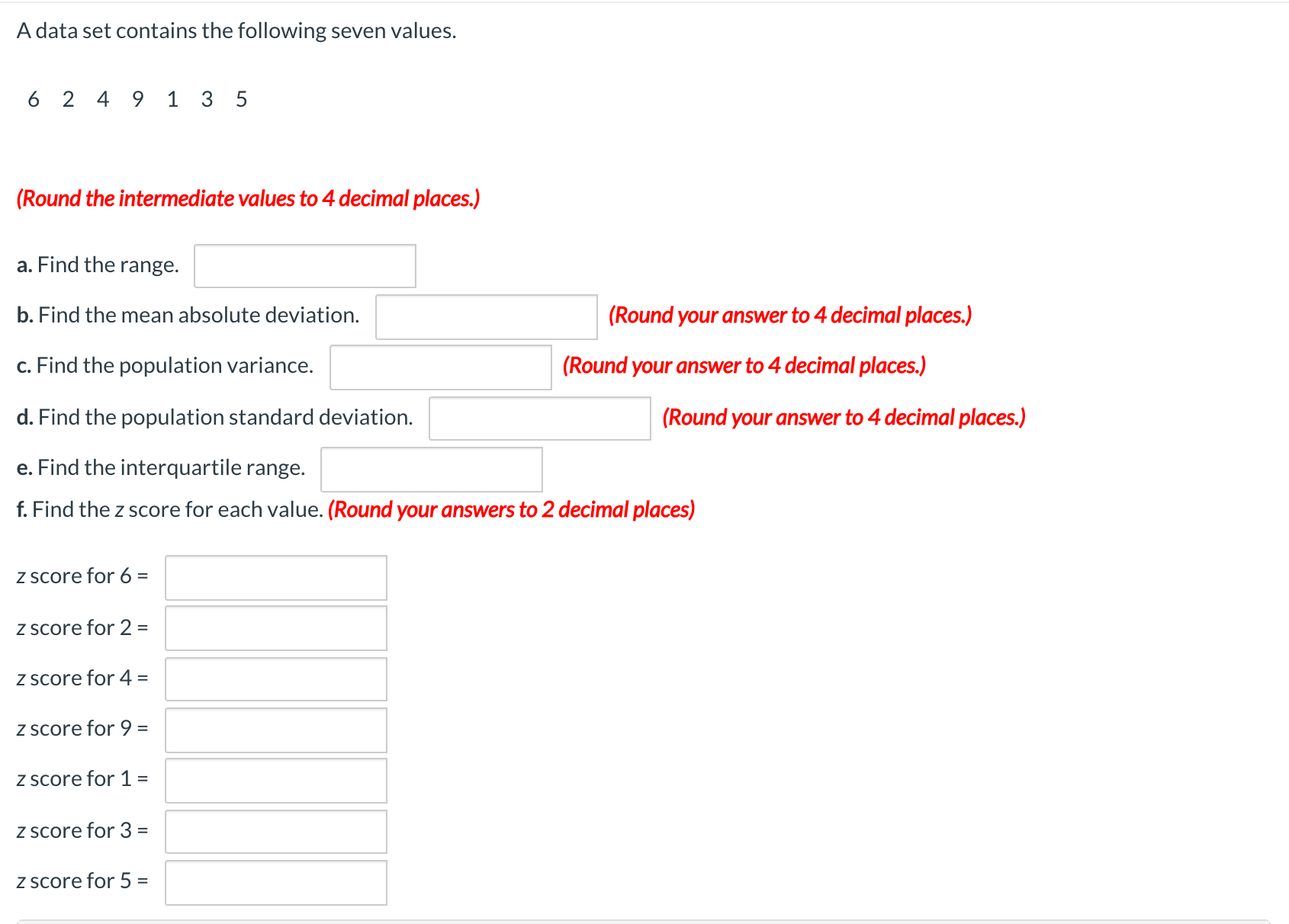
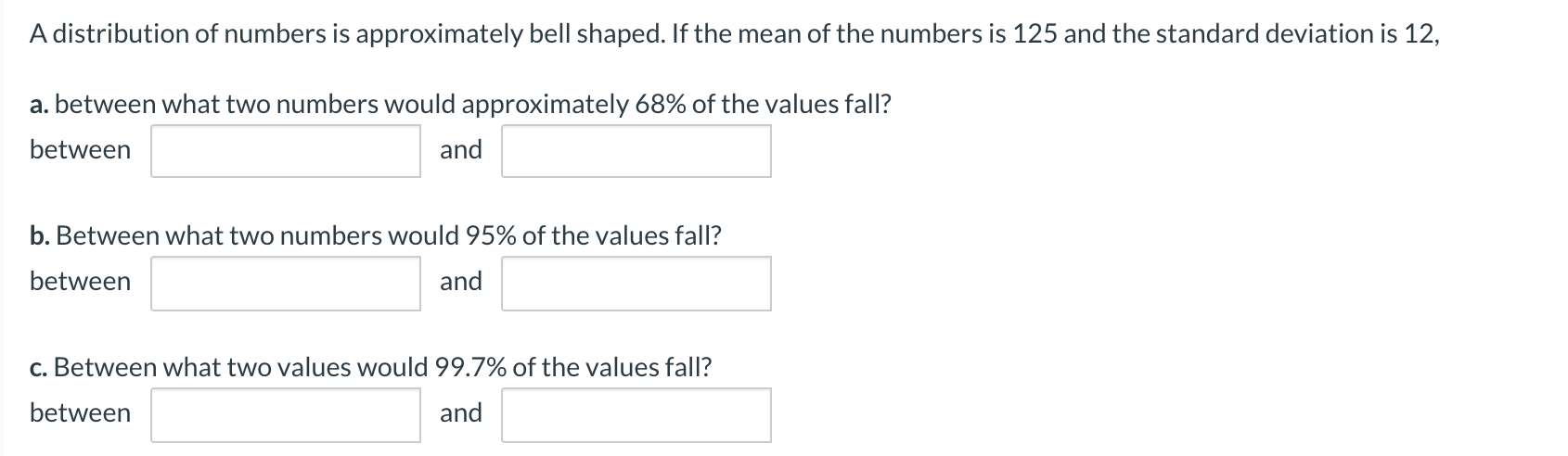
Some numbers are not normally distributed. If the mean of the numbers is 38 and the standard deviation is 6, what proportion of values would fall between 26 and 50? What proportion of values would fall between 14 and 62? Between what two values would 89% of the values fall? (Round your answers to 2 decimal places.) At least % of the values will fall between 26 and 50. At least 93,75 % of the values fall between 14 and 62. Between 20 and 56 at least 89% of the values fall. \fA data set contains the following seven values. 6249135 (Round the intermediate values to 4 decimal places.) 3. Find the range. ':| b. Find the mean absolute deviation. |:| (Round youranswer to 4 decimal places.) (2. Find the population variance. ':| (Round your answer to 4decimal places.) d. Find the population standard deviation. ':| (Round youranswer to 4decimal places.) e. Find the interquartile range. :I f. Find the z score for each value. (Round your answers to 2 decimal places) z score for 6 = z score for 2 = z score for 4 = z score for 9 = z score for 1 = z score for 3 = z score for 5 = According to Chebyshev's theorem, at least what proportion of the data will be within u + ko for each value of k? a. k = 2 75 (Round your answer to 2 decimal places, e.g.,0.12.) b. k = 2.5 84 (Round your answer to 2 decimal places, e.g.,0.12.) c. k = 1.6 87 (Round your answer to 3 decimal places, e.g.,0.123.) d. k = 3.2 89.59 (Round your answer to 3 decimal places, e.g.,0.123.)A distribution of numbers is approximately bell shaped. If the mean of the numbers is 125 and the standard deviation is 12, a. between what two numbers would approximately 68% of the values fall? between and b. Between what two numbers would 95% of the values fall? between and c. Between what two values would 99.7% of the values fall? between and
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


