1. Square roots modulo n;

(a) 9493² mod 11413 = 1. Check it if you dont believe me! Why does this prove that 11413 is composite?

(b) Use the equation in (a) to factor 11413. It is possible to do this with a computer by trial division because the numbers are relatively small, but I want you to show the steps of a computation that can be carried out by hand, or that could be done if the numbers given in (a) were many, many times larger.

(c) Similarly, carry out a calculation that will ?nd the other square roots of 1 modulo 11413. Of course, two of these square roots are 1 and 11412; ?nd another one.

2. Easy factorization if p,q are too close together:

This problem forms the theoretical basis for one of the computer problems below. (You do not need to prove the result here in order to tackle the computer problem, you can just accept it and apply the given algorithm.)

Suppose Alice decides to use primes of more than 200 decimal digits (i.e., greater than 10²⁰⁰) to generate her RSA modulus. She picks a prime p at random, and then chooses q to agree with p in all but the last 100 digits. Her reasoning is that p and q have effectively been randomly sampled from a set of size 10¹⁰⁰, and that it will be just as hard for an adversary to factor N = pq as it would be to factor the product of two random 100-digit primes. But Alice is in for a nasty surprise: If we have a factorization n = pq, then we can write the two primes as A?x and A+x, where A = (p+q)/2 is the average of p and q. Thus

N = pq = (A?x)(A + x) = A² ?x²,

so

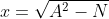
If we knew what A was, then since computing exact square roots is easy, we could determine x and hence the factors p and q. But how can we determine A without knowing p and q in the ?rst place?

Prove that in the circumstances described above, 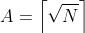, the smallest integer greater than 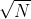. Thus we can factor N by solving the easy problem of computing the square root, which gives us A, and then x and the prime factors Ax.

HINT. The circumstances described above are that p and q differ by less than 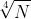. You need to prove that in this case .

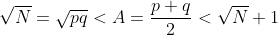Its easiest to do this if you look at what you get by squaring all parts of the inequality.

= A2 - N