Question: 1. Suppose that f is a function whose domain is R and satisfies the following properties: . f(x) = -1 when x > 2 .

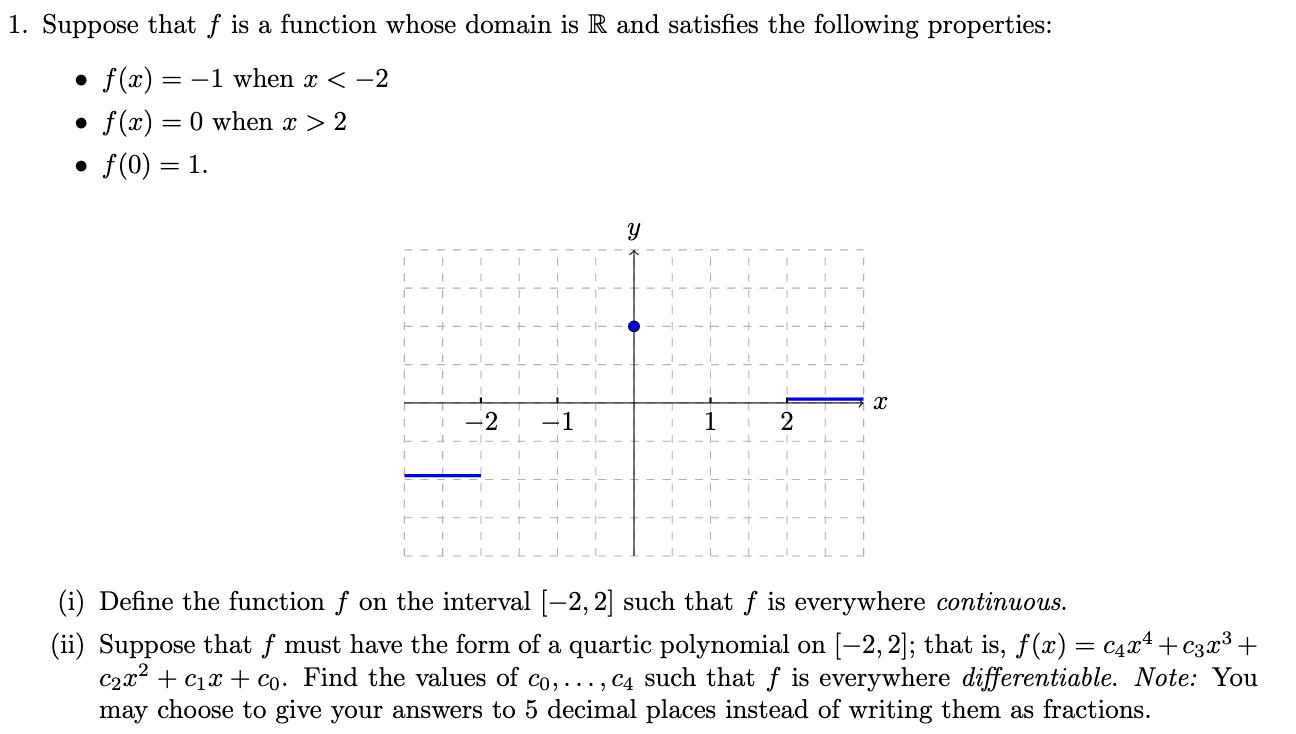
1. Suppose that f is a function whose domain is R and satisfies the following properties: . f(x) = -1 when x > 2 . f (0) = 1. y 2 (i) Define the function f on the interval [-2, 2] such that f is everywhere continuous. (ii) Suppose that f must have the form of a quartic polynomial on [-2, 2]; that is, f(x) = c424 + C323 + c2x2 + cix + co. Find the values of co, ..., c4 such that f is everywhere differentiable. Note: You may choose to give your answers to 5 decimal places instead of writing them as fractions

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Question 1. Suppose that f is a function whose domain is R and satisfies the following properties: . f(x) =0 when x 1 . f(0) = 1. y 1. Define the function f on the interval [-1, 1] such that f is...

Hi please help me with this questionPlease be specific in the solution. Thank you 1. Suppose that f is a function whose domain is R and satisfies the following properties: . f(x) = -1 when x 2 . f(0)...

Please answer each question thoroughly for a like Suppose that f is a function whose domain is R and satisfies the following properties: . f(x) = -1 when I 2 . f(0) = 1. (i) Define the function f on...

Hello, i will like help with this assignment. please use details and thank you 1. Suppose that f is a function whose domain is R and satises the following properties: 0 f(:c) = 1 whens: 2 o f(0) = 1....

Please explain your answer! Thanks for help! Question 1. Suppose that f is a function whose domain is R and satisfies the following properties: . f(x) =0 when x 1 . f(0) = 1. 1. Define the function f...

Please answer each step thoroughly Suppose that f is a function whose domain is R and satisfies the following properties: . f(x) = -1 when I 2 . f(0) = 1. (i) Define the function f on the interval...

Need answer and steps 1. Suppose that f is a function Whose domain is R and satises the following properties: o f(::) = 1 when I 2 o f(0) = 1. (i) Dene the function f on the interval [2, 2] such that...

1.Write an algorithm in pseudocode for each description of the input and output. (a) Input: a1, a2,...,an, a sequence of numbers, where n 1 n, the length of the sequence. Output: "True" if the...

Let f be a function whose domain is R. Suppose that for all x (1, 1), x2 f(x) |x|. Prove that limx0 f(x) = 0. Please use the epsilon-delta prove to prove this question.

Please do the circled questions For Exercises 19-56, assume f is a function whose domain is the interval [1, 5], whose range is the interval [1,3], and whose graph is the figure below. 3 N The graph...

Suppose that the hypotheses of Question 6.4.21 are to be tested with a decision rule of the form "Reject H 0 : = 2 if y 1 y 2 k." Find the value of k that gives a level of significance of 0.05.

Calculate the minimum size of trunking required to accommodate the following single core thermosetting insulated cables: 5x 1.5mm solid conductors 15 x 4.0mm 5x 10.0mm stranded conductors stranded...

You borrowed $ 1 3 , 5 0 0 from a bank. Interest is compounded annually and the annual interest rate is 3 . 1 3 % . Suppose you make a yearly repayment of $ 1 5 0 0 every year ( except the final...

The last step in the value creation and delivery sequence is ________ the value where the sales force, sales promotion, advertising, and other communication tools announce and promote the product....

Do not come to the conclusion too quickly

Engage everyone in the dialogue

1. Given your basic mental state, i.e. the state you often return to. Give this state a name that you recognize and that is easy to remember, such as irritability, frustration, joy, etc. Also give...