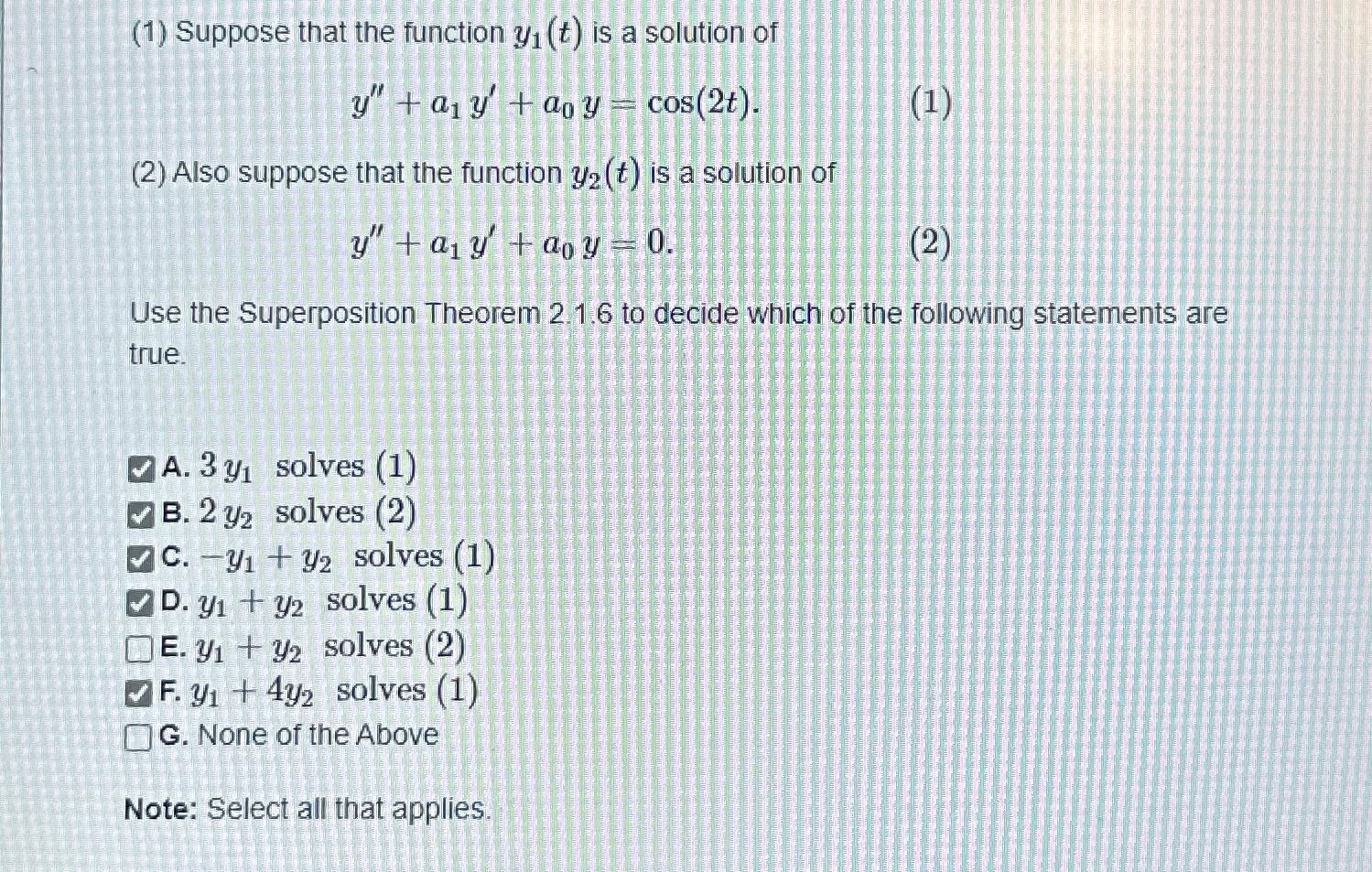
Question: (1) Suppose that the function y_(1)(t) is a solution of y^('')+a_(1)y^(')+a_(0)y=cos(2t). (2) Also suppose that the function y_(2)(t) is a solution of y^('')+a_(1)y^(')+a_(0)y=0.
(1) Suppose that the function
y_(1)(t)is a solution of\
y^('')+a_(1)y^(')+a_(0)y=cos(2t).\ (2) Also suppose that the function
y_(2)(t)is a solution of\
y^('')+a_(1)y^(')+a_(0)y=0.\ Use the Superposition Theorem 2.1.6 to decide which of the following statements are true.\ A.
3y_(1)solves
(1)\ B.
2y_(2)solves (2)\ C.
-y_(1)+y_(2)solves (1)\ D.
y_(1)+y_(2)solves
(1)\ E.
y_(1)+y_(2)solves (2)\ F.
y_(1)+4y_(2)solves (1)\ G. None of the Above\ Note: Select all that applies.
(1) Suppose that the function y1(t) is a solution of y+a1y+a0y=cos(2t). (2) Also suppose that the function y2(t) is a solution of y+a1y+a0y=0 Use the Superposition Theorem 2.1.6 to decide which of the following statements are true. A. 3y1 solves (1) B. 2y2 solves (2) C. y1+y2 solves (1) D. y1+y2 solves (1) E. y1+y2 solves (2) F. y1+4y2 solves (1) G. None of the Above Note: Select all that applies
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


